Способ задания движения, заключающийся в задании координат точки как известных функций времени, называется координатным способом задания движения и требует выбора конкретной системы координат (прямоугольной декартовой, цилиндрической, сферической). При движении точки в плоскости иногда используют полярные координаты.
Для прямоугольной декартовой системы координат задают координаты x, y, z точки M как известные функции времени.
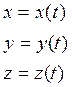 кинематические
уравнения движения в координатной форме
кинематические
уравнения движения в координатной форме
Траектория задана в параметрической форме.
3. Естественный (траекторный) способ. Задаются траектория точки и закон ее
движения по этой траектории. Пусть M0 – какая-либо
фиксированная точка на траектории. Выбрав направление положительного отчета
дуги по траектории, мы определим положение точки M в любой момент времени, если будем знать, как изменяется
дуга ![]() со временем.
со временем.
![]() - закон движения, G
– траекторная координата.
- закон движения, G
– траекторная координата.
Если движение происходит в сторону возрастания G , то дифференциал дуги ![]() . Если
движение в сторону убывания дуги, то
. Если
движение в сторону убывания дуги, то ![]() .
.
Путь S , проходимый точкой, всегда будет возрастать и, следовательно, положителен, то есть,
![]()
![]()
Все рассмотренные способы задания движения взаимосвязаны.
Пусть движение задано в координатной форме:
![]()
Перейдем к векторному способу. Введем ![]() , тогда:
, тогда:
![]()
Модуль ![]() :
:
![]()
Направление ![]() :
:
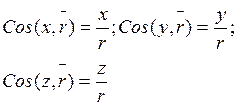
Скорость точки.
![]() 1. При векторном способе. Рассмотрим два
близких положения
1. При векторном способе. Рассмотрим два
близких положения ![]() на траектории.
на траектории.
Вектор ![]() - назовем вектором перемещения
точки за время ∆t . Отношение
- назовем вектором перемещения
точки за время ∆t . Отношение 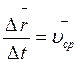 называется средней скоростью точки за
промежуток времени
называется средней скоростью точки за
промежуток времени ![]() .
.
Скоростью точки в данный момент времени называется предел отношения вектора перемещения точки к промежутку времени, за который произошло это перемещение, когда этот промежуток времени стремится к нулю, то есть,
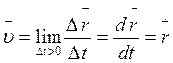
При перемещении ![]() секущая
секущая ![]() занимает
положение касательной, то есть, скорость направлена по касательной к траектории
в точке дифференцирования в сторону движения точки.
занимает
положение касательной, то есть, скорость направлена по касательной к траектории
в точке дифференцирования в сторону движения точки.
2. При координатном способе. Пусть движение задано в декартовой системе
координат, то есть, ![]()
![]()
Так как единичные векторы (орты) ![]() выбранной
системы координат – const, то
выбранной
системы координат – const, то 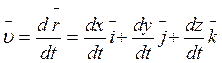
Вектор ![]() можно разложить на составляющие по осям
координат
можно разложить на составляющие по осям
координат
![]()
Тогда: 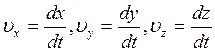
Проекция скорости точки на координатную ось равна первой производной по времени от соответствующей этой оси координаты.
Модуль скорости:
![]()
Направляющие косинусы:
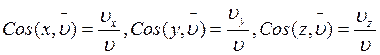
3. При естественном способе. Пусть точка M движется по кривой 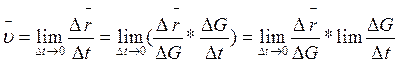
Так как предел отношения дуги к стягивающей ее хорде равен по модулю 1, а предельное положение секущей MM1 совпадает с направлением касательной к кривой в точке M, то
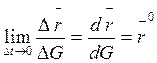 - единичный вектор касательной к кривой,
направленный в сторону положительного отсчета дуги.
- единичный вектор касательной к кривой,
направленный в сторону положительного отсчета дуги.
Так как 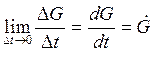
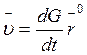
Обозначим: 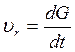 . Тогда:
. Тогда: ![]()
![]()
Так как проходимый точкой путь всегда положителен, то элемент пути ![]() , следовательно:
, следовательно:
![]()
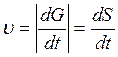
Ускорение точки.
1. При векторном способе. При криволинейном неравномерном движении
скорость точки меняется по величине и направлению. Отношение приращения вектора
скорости ![]() к промежутку времени
к промежутку времени ![]() называется ускорением точки за промежуток
времени
называется ускорением точки за промежуток
времени ![]() .
.
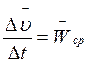
Ускорением ![]() точки в данный момент времени
называется предел отношения приращения скорости
точки в данный момент времени
называется предел отношения приращения скорости ![]() к
приращению времени
к
приращению времени ![]() при условии, что последнее
стремится к нулю, то есть,
при условии, что последнее
стремится к нулю, то есть, 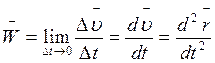
Ускорение точки в данный момент времени равно первой производной по времени от вектора скорости точки или второй производной по времени от радиуса – вектора точки.
2. При координатном способе. Пусть движение точки задано в прямоугольной
системе координат: ![]()
Так как ![]() , то
, то
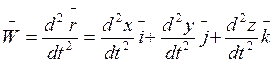 , но
, но
![]() .
.
Тогда:
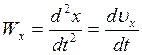
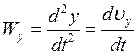
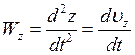
Модуль ускорения:
![]()
Направляющие косинусы вектора ускорения:
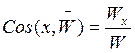
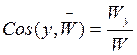
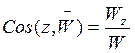
3. При естественном способе.
Пусть ![]() единичный вектор касательной, проведенный в
какой-либо точке M пространственной
кривой,
единичный вектор касательной, проведенный в
какой-либо точке M пространственной
кривой, ![]() в точке M1,
близкой к M.
в точке M1,
близкой к M.
Перенесем ![]() в точку M и проведем через
в точку M и проведем через ![]() плоскость. При
стремлении
плоскость. При
стремлении ![]() 1 к
1 к ![]() эта
плоскость в пределе займет определенное положение. Ее называют соприкасающейся.
эта
плоскость в пределе займет определенное положение. Ее называют соприкасающейся.
Плоскость, проведенную через ![]() перпендикулярно
перпендикулярно ![]() , называют нормальной.
, называют нормальной.
Линия пересечения соприкасающейся и нормальной плоскостей – главная нормаль.
Единичный вектор ![]() – в
сторону вогнутости кривой.
– в
сторону вогнутости кривой.
Плоскость, проведенная через ![]() перпендикулярно главной нормали
перпендикулярно главной нормали
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.