Динамика относительного движения. Частные случаи относительного движения. Теорема об изменении количества движения материальной точки

Динамика относительного движения.

Д.у. относительного движения материальной точки.

Кинематические характеристики в разных с.о. – разные. Основное уравнение динамики для инерциальной с.о.

 (1) - равнодействующая всех непосредственно приложенных к м.т. сил.

Обобщим его на случай относительного движения.

Система 0xyz – неподвижная (абсолютная); 0ξηζ – подвижная система координат.

Движение точки под действием силы - уравнение (1). Но для сложного движения:

 (2)

Подставим (2) в (1):

 (3)

Проанализируем правую часть. Условие физической однородности – все три слагаемые имеют размерность силы. Поэтому можно трактовать:

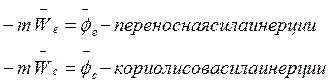 (4)

Силы  и  наблюдаются только в подвижной системе координат.

Тогда:  (5) – д.у. относительного движения материальной точки в векторной форме.

Относительное движение точки происходит под действием не только непосредственно приложенной силы , но и под действием переносной силы инерции Кориолиса . Уравнения (1) и (5) отличаются наличием действующих сил, но сохраняются по структуре.

Если спроецировать (5) на оси координат, то получим уравнения в координатной форме:

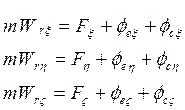
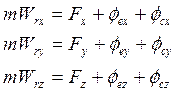
В абсолютной системе координат – если на точку не действуют силы, - точки в покое или прямолинейно движется. В относительной системе координат появляются силы инерции, которые приводят к ускоренному движению точки. Реальны ли силы инерции? 

Да, реальны (пример с тормозящим трамваем). Но этой силе нельзя сопоставить тело, являющееся ее источником. Нельзя этой силе сопоставить силу, противоположно направленную, не справедлив III закон Ньютона.

До сих пор не существует единой точки зрения.

Частные случаи относительного движения.

1). Пусть подвижная система координат перемещается поступательно, то есть:

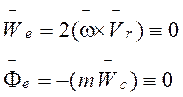
 (5^́)

2). Подвижная система координат перемещается поступательно, равномерно и прямолинейно, то есть оси параллельны осям неподвижной системы координат.

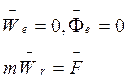 (5^˝)

Так как оси координат параллельны, то

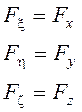
Уравнения (1) и (5^˝) – тождественны. Наблюдатель в замкнутом объеме, движущемся равномерно и прямолинейно, не ощущает сил инерции, у него нет объективных данных, позволяющих сказать о перемещении системы координат, связанной с объемом. Поэтому такая система координат называется инерциальной. То есть инерциальными системами координат называются такие системы, по отношению к которым материальное тело может получить ускорение только вследствие реального воздействия на него других тел, но не вследствие движения системы координат. Инерциальную систему координат можно определить как такую подвижную систему, по отношению к которой д.у. имеют тот же вид, который они имеют, когда система координат находиться в покое. В этом состоянии принцип относительности классической механики Галилея-Ньютона.

Нельзя сказать, что все характеристики движения в инерциальной системе движения одинаковы, так как одинаковы уравнения движения. Ускорения одни, скорости и траектории различны за счет различных н.у. (груз, сбрасываемый с самолета).

Действием сил инерции объясняются различные эффекты – закон Бэра: все реки, текущие в северном полушарии с юга на север по меридиану, имеют более крутой правый берег. Рассмотрим частицу воды со скоростью . На нее действует . отклоняет частицу к востоку, то есть действует на правый берег, .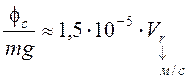

Двухколейная железная дорога – правый рельс изнашивается быстрее.

Основные теоремы динамики материальной точки.

Позволяют установить ряд законов, следующих из основного уравнения динамики материальной точки .

Важность основных теорем состоит в том, что с их помощью вводятся в рассмотрение новые величины, характеризующие движение материальной точки (динамические характеристики), например, кинетическая энергия. Они раскрывают действие силы на материальную точку за некоторый промежуток времени (импульс силы) и на данном перемещении ее (работа силы). Теоремы динамики устанавливают связь между динамическими характеристиками точки и действующими на нее силами, что дает возможность раскрыть природу механического движения с новых точек зрения.

Значение общих теорем динамики состоит еще и в том, что в ряде случаев они подводят нас к возможности получения первых интегралов д.у. движения.

Теорема об изменении количества движения материальной точки.

Пусть материальная точка М массы m движется относительно выбранной системы отсчета и в момент времени t имеет скорость .

Количеством движения материальной точки, отвечающим моменту времени t, называется векторная физическая величина, равная произведению массы этой точки на ее скорость в рассматриваемый момент времени

Из определения следует, что:

1)  количество движения всегда направлено в ту же сторону, что и скорость точки (m>0)

2)  количество движения изображается закрепленным вектором, имеющим начало в данной точке.

3)  количество движения может быть записано в проекции на оси координат 0xyz, неизменно связанных с выбранной системой отсчета.

Алгебраические величины проекций количества движения материальной точки на оси координат , ,  называются так же количеством движения материальной точки по направлениям осей соответственно, в момент времени t.