Динамика относительного движения. Частные случаи относительного движения. Теорема об изменении количества движения материальной точки, страница 2

Частный случай – закон сохранения количества движения материальной точки.

Если равнодействующая всех сил, приложенных к материальной точке, равна нулю

-количество движения материальной точки сохраняется неизменным по величине и направлению.

В этом случае материальная точка с постоянной по направлению и величине скоростью (по инерции).

Действие силы на материальную точку в течение времени dt можно охарактеризовать так называемым элементарным действием силы . Полный импульс силы за время t определяется по формуле:

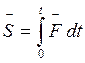
Проекции импульса силы на оси декартовой системы:

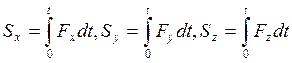
Рассмотрим д.у. движения точки m под действием силы (или равнодействующей всех сил, приложенной к материальной  точке):

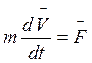
Так как масса точки принимается постоянной, то ее можно ввести под знак производной:

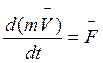
Это уравнение выражает теорему об изменении количества движения в дифференцированной форме: производная по времени от количества движения точки равна действующей на точку силе.

В проекциях на координатные оси:

.

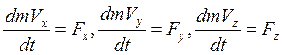Если обе части уравнения умножить на , то получим другую форму этой же теоремы – теорему импульсов в дифференциальной форме:

 - дифференциал количества движения тогда равен элементарному импульсу силы, действующей на точку.

Интегрируя обе части уравнения в пределах от 0 до t, имеем:

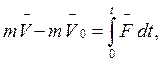
где  - скорость в конечный момент времени, - скорость в начальный момент t=0. Это уравнение выражает теорему об изменении количества движения материальной точки в конечной (или интегральной) форме: изменение количества движения точки за некоторый промежуток времени равно импульсу силы за тот же промежуток времени.

В проекциях на оси:

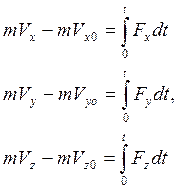
В общем случае:

Если функция только времени, то интегралы могут быть вычислены и получены первые уравнений движения.

Уравнения показывают, что изменение проекции количества движения материальной точки на данную ось за некоторый промежуток времени равно проекции на эту же ось импульса приложенной к точке силы за тот же промежуток времени.

Теорема об изменении момента количества движения материальной точки относительно неподвижного полюса.

Для материальной точки массой m, движущейся со скоростью , моментом количества движения (кинетическим моментом) относительно неподвижного центра 0 называется момент вектора  относительно этой точки:

Проекции момента относительно осей декартовой системы координат будут:

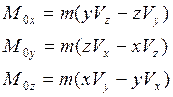
Момент количества движения приложен в (.)0, относительно которой он вычисляется.

Пусть движение материальной точки M происходит под действием силы (или системы сил (_{1, 2,… n}), равнодействующая которых ) и ее уравнения движения:

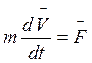
Проведем из произвольного центра О в точку радиус-вектор  и умножим обе части уравнения слева на вектор :

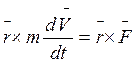
В правой части формулы имеется момент силы относительно неподвижной (.)0. Преобразуем левую часть:

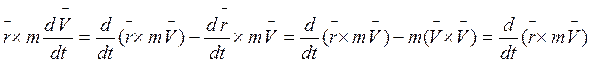
Тогда:

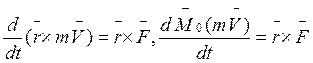
Это соотношение выражает теорему об изменении момента количества движения материальной точки относительно центра: производная по времени от момента количества движения материальной точки относительно некоторого неподвижного центра равна моменту силы, приложенной к точке, относительно того же центра.

Проецируя на оси, получаем теоремы об изменении момента количества движения точки относительно осей координат:

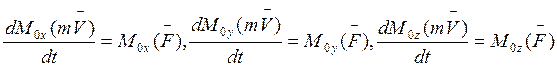
В развернутой форме:

 (*)

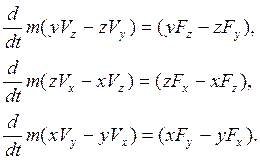Производная по времени от момента количества движения материальной точки относительно некоторой неподвижной оси равна моменту силы, действующему на точку, относительно той же оси.

Как видно из уравнений (*) при их интегрировании необходимо вычисление интегралов от правых частей, для этого нужно знать . Но тогда отпадает надобность в применении равенств (*). Но существуют случаи, когда теорема дает возможность эффективно решать задачи динамики.

К ним относится случай действия центральной силы – сила, линия действия которой проходит через некоторую фиксированную точку пространства (полюс). Например, при изучении движения Земли в Солнечной системе на Землю действует сила притяжения Солнца, все время направленная к центру Солнца.

Момент центральной силы относительно центра тождественно равен нулю.

Частные случаи.

1.

То есть  во все время движения материальной точки, равный его значению при t=0, то есть - закон сохранения момента количества движения. Из него следует, что:

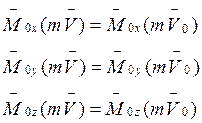, то есть, имеем три первых интеграла движения.

Закон сохранения количества движения – иначе закон площадей.

Секторная скорость: 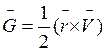 - вектор, характеризующий быстроту изменения площади поверхности, описываемой радиусом-вектором.

То есть в случае действия центральной силы секторная скорость – const, то есть радиус-вектор точки описывает равные площади в любые одинаковые промежутки времени. Кроме того, траектория точки является плоской кривой. В самом деле, вектор  сохраняет постоянное направление в пространстве. Из формулы, определяющей , следует, что  все время расположен в плоскости, перпендикулярной , то есть траектория точки лежит в этой плоскости.

2. Если момент силы относительно некоторой оси равен 0:

, то

Это, в частности, будет, когда внешняя сила параллельна оси или ее пересекает.