Санкт-Петербургский Государственный Морской Технический Университет
Кафедра физики
Курсовая работа
по теоретической физике
на тему:
«Исследование средней работы вынуждающей силы действующей на гармонический осциллятор»
выполнил студент группы 7240
Курячий Вадим проверил преподаватель
Монозон Б.С
г.Санкт-Петербург
2008г.
Содержание
1.Теоретическая часть
2.Практическая часть
2.1 Формулировка задачи
2.2Решение задачи
2.2.1Первая часть
2.2.2Вторая часть
2.2.3Третья часть
Список используемой литературы
Графическое приложение
1.Теоретическая часть
Вынужденные колебания -это колебания происходящие под действием вынуждающей силы.
В общем случаи их уравнение будет иметь вид
![]() (1)
(1)
Где ![]() -жесткость,
-жесткость, ![]() составляющая силы сопротивления,
составляющая силы сопротивления,![]() -вынуждающая сила.
-вынуждающая сила.
Средняя работа этой вынуждающей силы определяется формулой
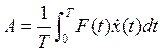 (2)
(2)
Где![]() -время за которое совершался колебательный
процесс
-время за которое совершался колебательный
процесс
Для одного полного колебания это время будет равно периоду гармонического колебания
,т.е
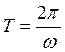 (3)
(3)
Уравнение (1) поделив на массу можно записать в виде
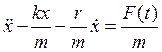 (4)
(4)
Собственная частота гармонических колебаний будет определятся формулой
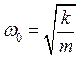 (5)
(5)
А коэффициент затухания колебаний
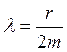 (6)
(6)
Тогда уравнение (4) можно записать в виде
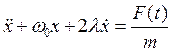 (7)
(7)
Решение этого уравнения![]() , а
вернее его производная по времени при подстановке в формулу (2) и позволит нам
вычислить среднюю работу.
, а
вернее его производная по времени при подстановке в формулу (2) и позволит нам
вычислить среднюю работу.
2.Практическая часть
2.1 Формулировка задачи
На осциллятор с трением(
собственная частота ![]() ,сила трения
,сила трения ![]() ) действует вынуждающая сила
) действует вынуждающая сила ![]()
а) Найти среднюю работу ![]() этой силы при установившихся колебаниях,
если
этой силы при установившихся колебаниях,
если ![]()
б) То же для 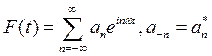
в) Найти среднюю работу за большой
промежуток времени силы ![]() при установившихся
колебаниях.
при установившихся
колебаниях.
г) Найти полную работу силы 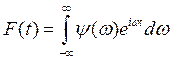 ,
,![]() если осциллятор при
если осциллятор при ![]() покоился.
покоился.
2.2 Решение задачи
2.2.1Первая часть
Известно что среднюю работу можно вычислить по следующей формуле
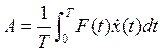 (1)
(1)
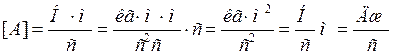
Займемся решением первой
части задачи, где вынуждающая сила равна ![]() (2)
(2)
Промежуток времени ![]() будет
равен периоду установившихся колебаний, а именно
будет
равен периоду установившихся колебаний, а именно
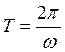 (3)
(3)
Как видно нам не хватает только одного элемента ![]() , который мы будем искать из уравнения
вынужденных гармонических колебаний полученного из уравнения движения
, который мы будем искать из уравнения
вынужденных гармонических колебаний полученного из уравнения движения
![]() (4)
(4)
где ![]() -сила сопротивления,
-сила сопротивления,![]() -сила трения,
-сила трения,![]() вынуждающая
сила(2)
вынуждающая
сила(2)
Разделив обе части уравнения (4) на ![]() , получим уравнение вынужденных
колебаний
, получим уравнение вынужденных
колебаний
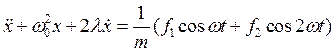 (5)
(5)
Итак, мы имеем дифференциальное уравнение , решение
которого![]() будет состоять из двух решений
будет состоять из двух решений
![]() (6)
(6)
где ![]() -общее решение
однородного дифференциального уравнения,
-общее решение
однородного дифференциального уравнения, ![]() частное решение
неоднородного уравнения
частное решение
неоднородного уравнения
Общее решение будет иметь вид
![]() (7)
(7)
Подставляя его в однородное уравнение , получим
![]() (8)
(8)
Решая квадратное уравнение получим
![]() (9)
(9)
Так как ![]() ,то
,то
![]() (10)
(10)
где ![]()
Тогда общее решение будет
![]() (11)
(11)
Преобразовывая получим
![]() (12)
(12)
Где ![]() - амплитуда затухающих
колебаний.
- амплитуда затухающих
колебаний.
Очевидно, что со временем ![]() убывает
убывает
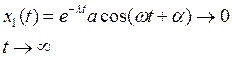
Теперь же перенесем свое внимание на частное решение
уравнения![]()
Рассмотрим уравнение
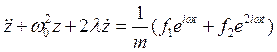 (13)
(13)
Очевидно что частным решением уравнения(5) будет действительная часть частного решения уравнения(13)
![]() (14)
(14)
Частное решение уравнения (13) будет иметь вид
![]() (15)
(15)
Подставив (15) в (13) и сгруппировав, получим
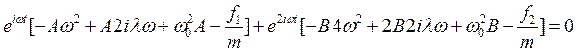 (16)
(16)
Отсюда
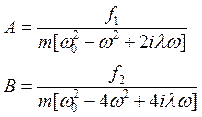 (17)
(17)
домножив на комплексно сопряженные выражения получим
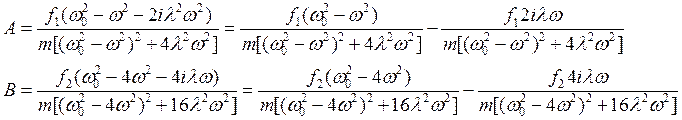 (18)
(18)
Учитывая формулу Эйлера запишем (15)
![]() (19)
(19)
Подставим (18) в (19)
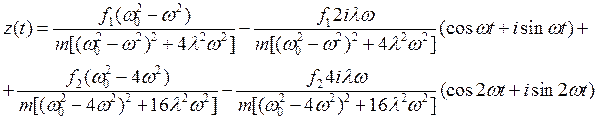 (20)
(20)
Раскрыв скобки и получим как комплексные , так и действительные члены.
Нас будут интересовать только действительные значения при 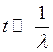
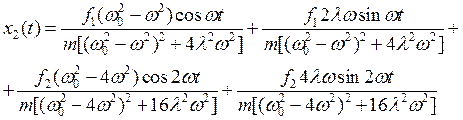 (21)
(21)
Так как мы показали выше что ![]() убывает
со временем, то
убывает
со временем, то
![]() (22)
(22)
Вычислим производную от (22)
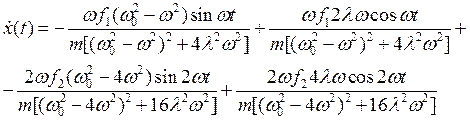 (23)
(23)
Перейдем к вычислению средней работы. Вычислим сначала подынтегральное выражение
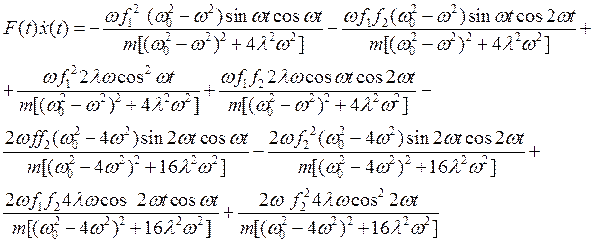 (24)
(24)
Подынтегральное выражение состоит из 8 членов, имеющих следующие
зависящие от ![]() элементы:
элементы:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() и
и![]()
Поскольку
![]()
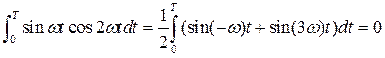
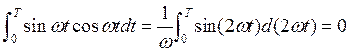
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.