Т.о. формулу 1 можно записать как
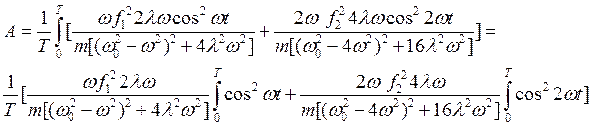 (25)
(25)
И нам остается только посчитать интегралы
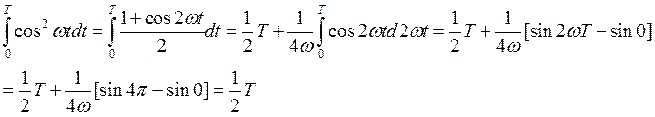
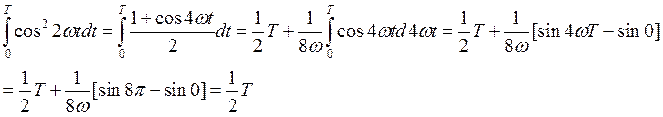
Подставив их в формулу(25) и вынеся общий множитель получим окончательный результат
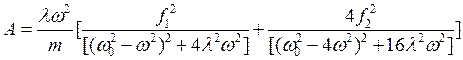
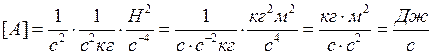 (26)
(26)
2.2.2 Вторая часть
Теперь же приступим к решению второй части данной задачи ,условия которой отличаюся от первой только видом вынуждающей силы
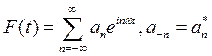 (27)
(27)
Уравнение вынужденных колебаний на основ5е формул (5) и (27) будет иметь вид
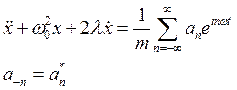 (28)
(28)
Рассмотрим его при ![]()
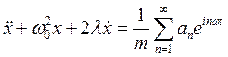 (29)
(29)
Как было показано выше обший член решение этого уравнения со временем исчезнет , т.е
![]() (30)
(30)
Частное решение уравнения (29) будет иметь вид
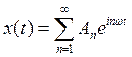 (31)
(31)
Подставив его в (29)получим
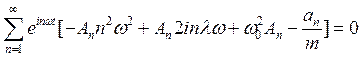 (32)
(32)
Отсюда
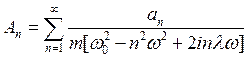 (33)
(33)
Учитывая формулу Эйлера (19)запишем (31)
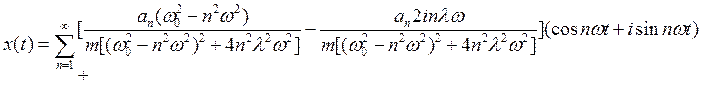 (34)
(34)
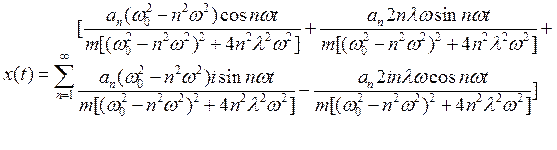 (35)
(35)
При ![]()
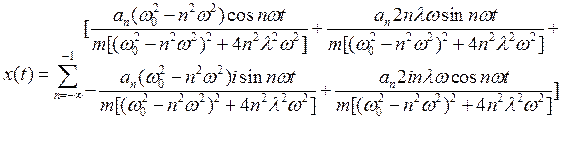 (36)
(36)
Тогда полная сумма будет равна
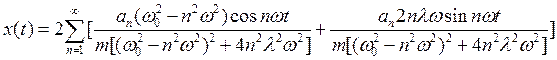 (37)
(37)
Вычислим производную от (37)
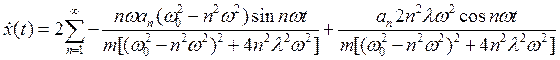 (38)
(38)
Рассмотрим вынуждающую силу для ![]() и
и ![]() при условии
при условии ![]()
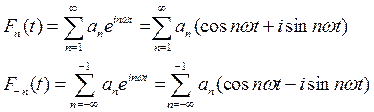 (39)
(39)
![]() Тогда полная сумма будет
выглядеть как
Тогда полная сумма будет
выглядеть как
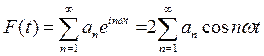 (40)
(40)
Перейдем к вычислению средней работы. Вычислим сначала подынтегральное выражение
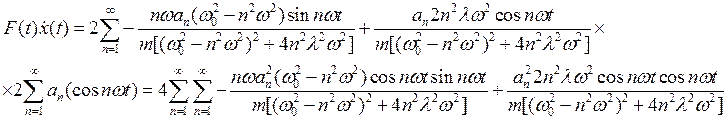 (41)
(41)
Из формулы один средняя работа будет равна
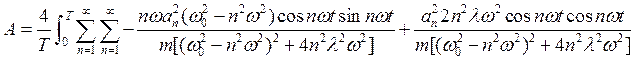 (42)
(42)
Выше было показано что так как 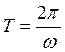 (
формула 3) перекрестные произведения произведения и произведения функций с
различными аргументами при интегрировании обнуляются, таким образом формула
средней работы примет вид
(
формула 3) перекрестные произведения произведения и произведения функций с
различными аргументами при интегрировании обнуляются, таким образом формула
средней работы примет вид
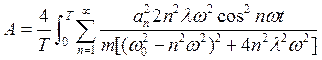 (43)
(43)
Нетрудно показать что
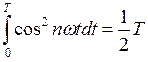
Интегрируя получим
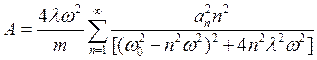 (44)
(44)
2.2.3 Третья часть
Перейдем к решению третьей задачи и попытаемся найти среднюю работу за длительный промежуток времени. Для этого будем пользоваться схожими с решением первой части задачи методами. Так же как и в первой задаче(1) работа будет равна
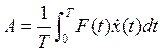
Однако время , по условию, длительное а следовательно его
можно записать в виде![]()
Вынуждающая сила будет равна
![]() (45)
(45)
Элемент ![]() мы будем искать из
уравнения движения(4), которое мы представим в виде
мы будем искать из
уравнения движения(4), которое мы представим в виде
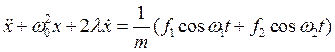 (46)
(46)
Как было показано при решении первой части задачи корнем общее решение этого уравнения со временем исчезает и справедлива формула (22)
![]()
Для того чтобы найти частное решение ![]() рассмотрим
уравнение
рассмотрим
уравнение
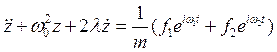
Действительная часть решения которого и будет ![]()
![]()
Частное решение уравнения будет иметь вид
![]()
Подставив его в уравнение и сгруппировав получим
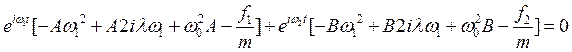 (47)
(47)
Отсюда
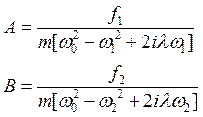 (48)
(48)
Домножив на комплексно сопряженные выражения получим
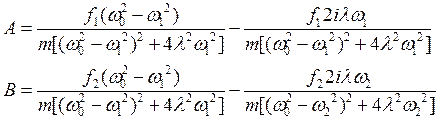 (49)
(49)
Подставив
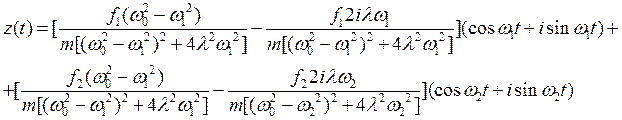 (50)
(50)
Раскрыв скобки и получим как комплексные , так и действительные члены. Но согласно
(14)
нас будут интересовать только действительные значения
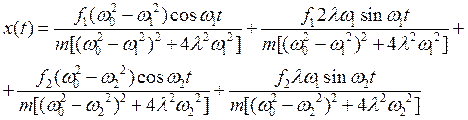 (51)
(51)
Вычислим производную от ![]()
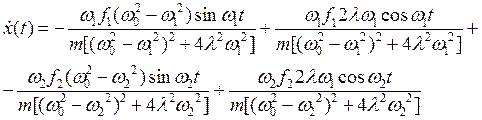 (52)
(52)
Перейдем к вычислению средней работы. Вычислим сначала подынтегральное выражение
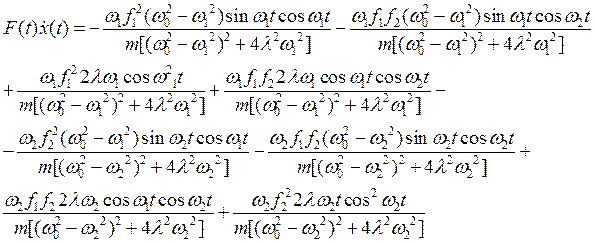 (53)
(53)
Подынтегральное выражение состоит из 8 членов, имеющих
следующие зависящие от ![]() элементы:
элементы:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() и
и![]()
Можно показать, что при вычислении работы члены содержащие перекрестные произведения синуса и косинуса или же функций одного вида но с различными аргументами обнуляются
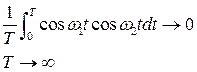
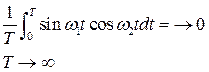
А теперь вычислим работу с двумя оставшимися членами
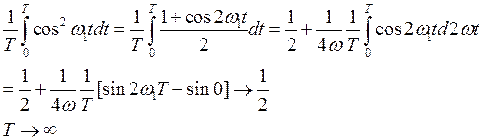
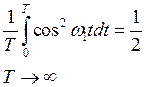
И с учетом полученных выше результатов и формулы (1) получим формулу средней работы за большой промежуток времени
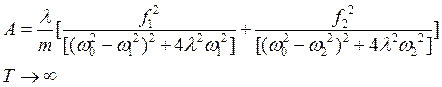 (54)
(54)
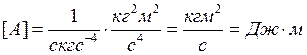
Список литературы
1.Бронштейн И.Н. Семиндяев К.А.Справочник по математике ,М.«Наука» 1964г.
2.Голдштейн Г. Классическая механика. М.»Наука» 1976г.
3.Ландау Л.Д, Лифшиц Е.М. ,Краткий курс теоретической физики М. «Наука» 1969г.
4.Савельев И.В. Курс общей физики т.1. М. «Наука» 1982г.
5.Иродов И.Е. Механика. Основные законы. М. «Просвещение» 1999г.
Графическое приложение
Зависимость средней работы за период( формула (1) и (3)) от
частоты вынуждающей силы![]() ( в случае кратных
частот)
( в случае кратных
частот)
При различных значениях ![]() (
(![]() )
)
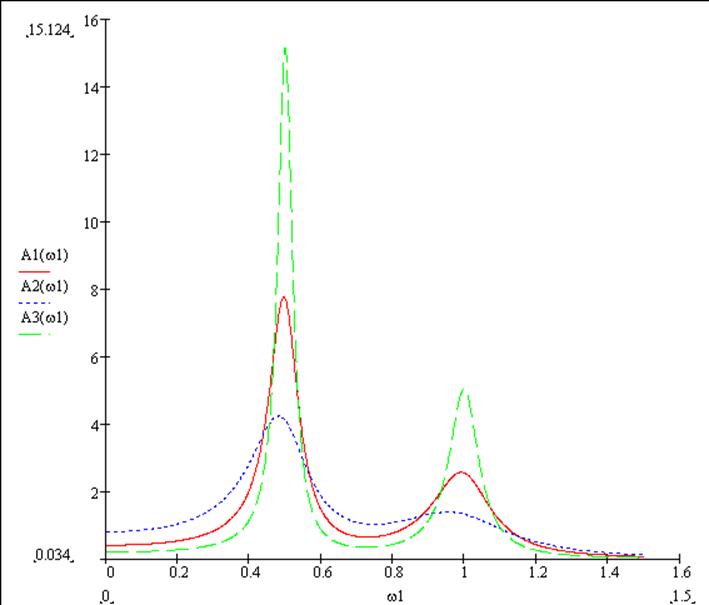
График построен при значениях вынуждающих сил ![]() и
и![]() , массы
, массы
![]() ,собственной частоты
,собственной частоты ![]() , частоты первой вынуждающей силы
, частоты первой вынуждающей силы ![]() и второй
и второй ![]() , где
значения
, где
значения ![]() изменяются от 0 до 1,6 рад/с,
изменяются от 0 до 1,6 рад/с,
Как видно из графика , что при меньших значениях ![]() значение средней работы будете большим,
причем при увеличении этого параметра ее максимумы будут смешаться вправо.Те
же самые свойства очевидны и для двух других графиков.
значение средней работы будете большим,
причем при увеличении этого параметра ее максимумы будут смешаться вправо.Те
же самые свойства очевидны и для двух других графиков.
Зависимость средней работы за большой промежуток времени (![]() )от частоты второй силы
)от частоты второй силы![]()
При различных значениях ![]() (
(![]() )
)
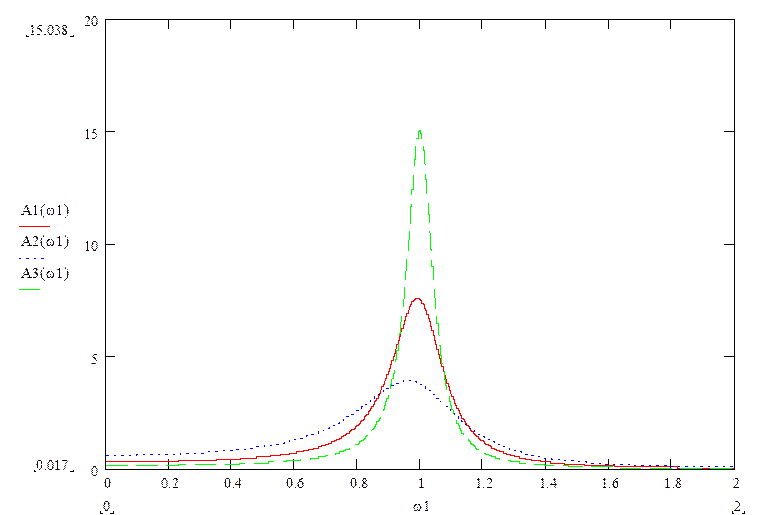
График построен при значениях вынуждающих сил ![]() и
и![]() , массы
, массы
![]() ,собственной частоты
,собственной частоты ![]() , частоты второй вынуждающей силы
, частоты второй вынуждающей силы ![]() и первой
и первой ![]() , где
значения
, где
значения ![]() изменяются от 0 до 2 рад/с,
изменяются от 0 до 2 рад/с,
Зависимость средней работы за большой промежуток времени (![]() ) от частоты второй силы
) от частоты второй силы![]()
При различных значениях ![]() (
(![]() )
)
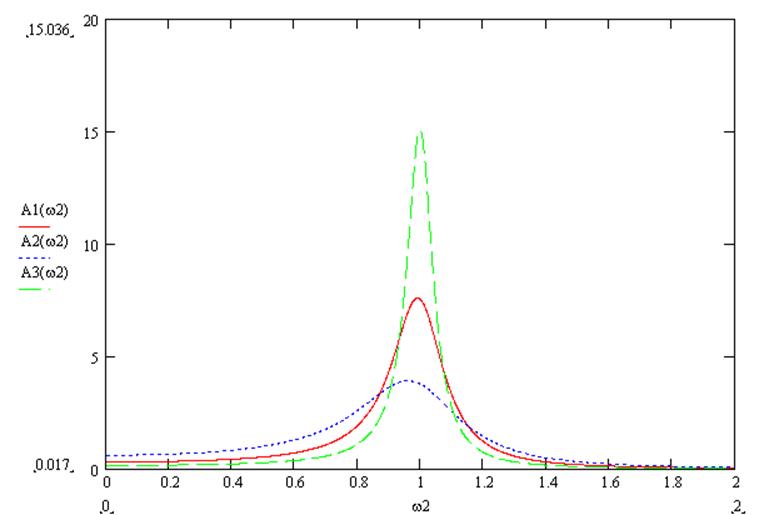
График построен при значениях вынуждающих сил ![]() и
и![]() , массы
, массы
![]() ,собственной частоты
,собственной частоты ![]() , частоты первой вынуждающей силы
, частоты первой вынуждающей силы ![]() и первой
и первой ![]() , где
значения
, где
значения ![]() изменяются от 0 до 2 рад/с,
изменяются от 0 до 2 рад/с,
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.