Кинематические уравнения Эйлера
Совокупность n вращений вокруг пересекающихся в одной точке осей эквивалентна одному вращению с мгновенной угловой скоростью.
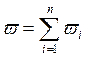
Полученное правило позволит выразить проекции мгновенной угловой скорости тела, имеющего одну неподвижную (.)О, через углы Эйлера и их производные.
Положение подвижной с.к. ![]() , жестко связанной с
телом, полностью определяется относительно неподвижной с.к.
, жестко связанной с
телом, полностью определяется относительно неподвижной с.к. ![]() углами Эйлера θ, ψ, φ. Абсолютная угловая скорость
углами Эйлера θ, ψ, φ. Абсолютная угловая скорость ![]() тела:
тела:
![]()
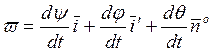 *)
*)
Модуль угловой скорости:
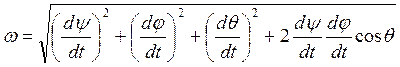
Составим таблицу направляющих cos единичных
векторов ![]() в системе подвижных осей
в системе подвижных осей ![]() **))
**))
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
0 |
|
|
0 |
|
|
Проецируя обе части (*) на оси ![]() и учитывая таблицу cos, найдем:
и учитывая таблицу cos, найдем:
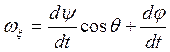
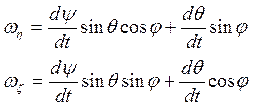
Аналогично можно найти проекции вектора угловой скорости на неподвижные оси координат.
**) Разложим единичный вектор ![]() на две
взаимноперпендикулярные составляющие, направив одну из них на оси ξ (она
равна
на две
взаимноперпендикулярные составляющие, направив одну из них на оси ξ (она
равна ![]() ), вторая составляющая, равная произведению
sinθ на единичный вектор вспомогательной оси будет
находиться в плоскости
), вторая составляющая, равная произведению
sinθ на единичный вектор вспомогательной оси будет
находиться в плоскости ![]() . Вспомогательная ось
составляет с осями η и ζ углы
. Вспомогательная ось
составляет с осями η и ζ углы ![]() и
и
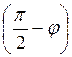 .
.
Регулярная прецессия
В процессе движения: ![]()
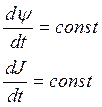
![]()
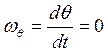
![]()
Вектор ![]() лежит в плоскости
лежит в плоскости ![]() .
.
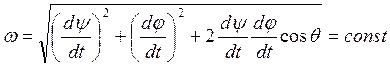
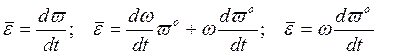
![]() - единичный вектор, направленный по
- единичный вектор, направленный по ![]() .
.
![]() , т.е.
, т.е. ![]() – по
линии углов производная вектора
– по
линии углов производная вектора ![]() , имеющего закрепленную
точку
, имеющего закрепленную
точку
![]() - скорость (.) К. Для (.) К угловая
скорость
- скорость (.) К. Для (.) К угловая
скорость ![]() , а радиус- вектор
, а радиус- вектор ![]() .
.
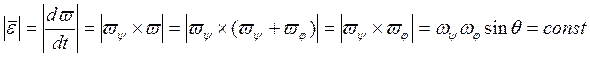 - по величине
- по величине
При регулярной процессии угловая скорость и угловое ускорение построены по величине и перпендикулярны.
Общий случай движения свободного твердого тела
Твердое тело произвольным образом перемещается в пространстве.
Oxyz - неподвижная, базовая с.к.
Выбираем производно (.)Р за полюс и свяжем с ней две с.к.
![]() - перемещается поступательно по
отношению к базовой
- перемещается поступательно по
отношению к базовой
![]() - жестко связана с телом.
- жестко связана с телом.
По отношению системы ![]() тело вращается вокруг
неподвижной точки Р, его положение определено углами φ, ψ, θ .
тело вращается вокруг
неподвижной точки Р, его положение определено углами φ, ψ, θ .
Положение системы ![]() по отношению к
базовой определено координатами
по отношению к
базовой определено координатами
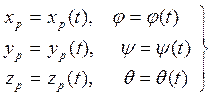 Кинематические уравнения движения
твердого тела
Кинематические уравнения движения
твердого тела
Твердое тело, произвольно движущееся в пространстве обладает шестью степенями свободы
Движение точки относительно систем координат, перемещающихся друг относительно друга.
Пример: движение самолета прямолинейное с ![]() движение
груза относительно 2-х наблюдателей.
движение
груза относительно 2-х наблюдателей.
В некоторых случаях целесообразно изучать движение точки одновременно по отношению к двум системам координат, одна из которых совершает заданное движение по отношению к другой (основной), принимаемой за неподвижную.
Сложным или абсолютным движением точки называется ее движение по отношению к системе координат, выбранной за основную.
Движение точки по отношению к подвижной системе отсчета называется относительным движением точки.
Движение подвижной системы отсчета по отношению к основной называется переносным движением.
Абсолютная и относительная производные от вектора
Пусть вектор ![]() определен в подвижной системе
координат, т.е. проекции его ax, ay, az
на оси подвижной системы – заданные функцией времени. Если
определен в подвижной системе
координат, т.е. проекции его ax, ay, az
на оси подвижной системы – заданные функцией времени. Если ![]() - единичные векторы подвижной системы
координат, то
- единичные векторы подвижной системы
координат, то
![]()
Абсолютная производная вектора ![]() по
времени:
по
времени:
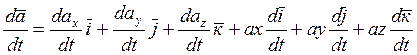
Сумма первых трех слагаемых – производная от ![]() в
подвижной системе координат называется относительной или локальной производной
и обозначается
в
подвижной системе координат называется относительной или локальной производной
и обозначается ![]() , т.е.
, т.е.
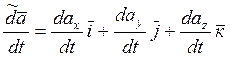
Производная по времени от вектора постоянного модуля по скалярному аргументу равна:
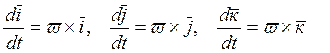
Т.е.
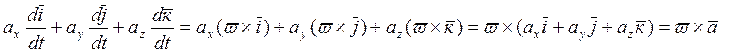
где ![]() - угловая скорость подвижной системы
координат.
- угловая скорость подвижной системы
координат.
Следовательно:
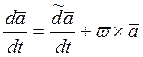
Абсолютная производная вектора равна сумме относительной производной этого вектора и векторного произведения угловой скорости подвижной системы координат на этот вектор.
Теорема о сложении скоростей
Рассмотрим движущуюся (.)М
Ox1y1z1 - неподвижная с.к.
Pxyz - подвижная с.к
Скорость (.)М по отношению к основной с.к. называется абсолютной
скоростью - ![]() . Скорость
. Скорость ![]() точки
по отношению к подвижной с.к. называется относительной скоростью.
точки
по отношению к подвижной с.к. называется относительной скоростью.
Переносной скоростью точки называют скорости той точки подвижной с.к., с которой в данный момент совпадает движущаяся точка.
(.) М при своем движении относительно подвижного тела, с которым жестко связана подвижная с.к., проходит через разные точки этого тела, имеющие отличные друг
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.