Момент инерции однородной материальной (вещественной) окружности («кольца»). Теорема Гюйгенса- Штейнера

Момент инерции плоского тела, у которого одни размер малы по сравнению  с двумя другими

Тв.т.  пренадлеж. плоскости ХОУ: Z=0

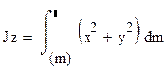
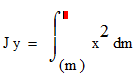
Jz =Jo=Jx +Jy - (42) для плоского тела пренадлеж. плоскости  ХОУ.

Частные случаи:

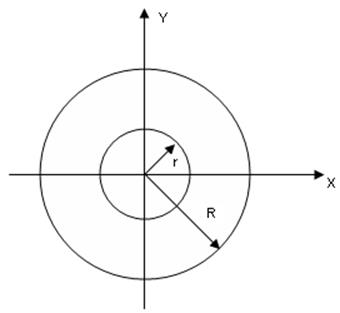
Момент инерции однородной материальной (вещественной) окружности («кольца»).

Дано:

m,R

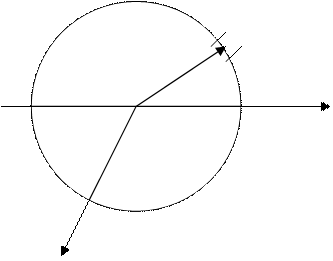Опр:Jz ,Jo,Jx ,Jy  

У                                  

dm

Х

Z

Т.к. окружность –плоское тело и пренадлежит плоскости ХОУ, то   Jz = Jo

Jx + Jy = Jo.

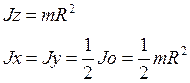                               (43)

2.Момент инерции сплошного (однородного) диска (круга).

Дано:

m,R

Опр:

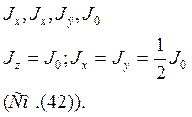
Круг «разбиваем» на б.б. число б. малых элементов концентрическими окружностями.

 

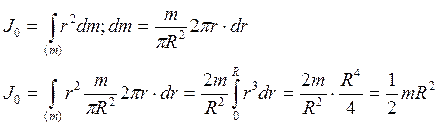
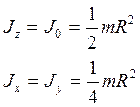  (44)

3.Момент инерции однородного шара (сферы).

Дано:

m,R

Опр:

Для шара:

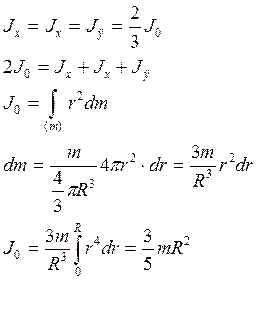
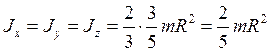  (45)

4.Момент инерции однородного тела сращения.

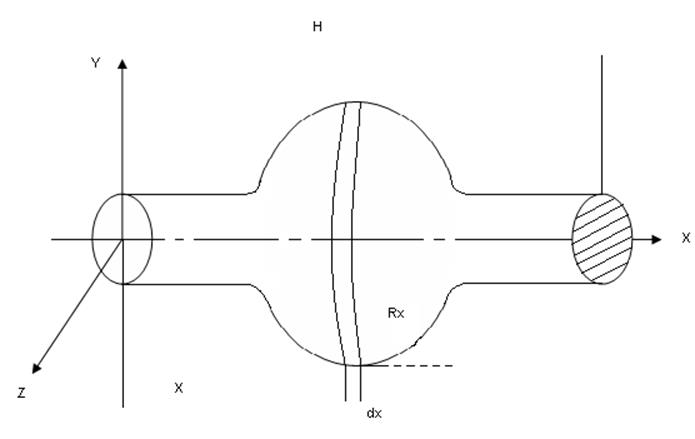
Дано:

m, H,

W-объемное тело

Опр:

Jx

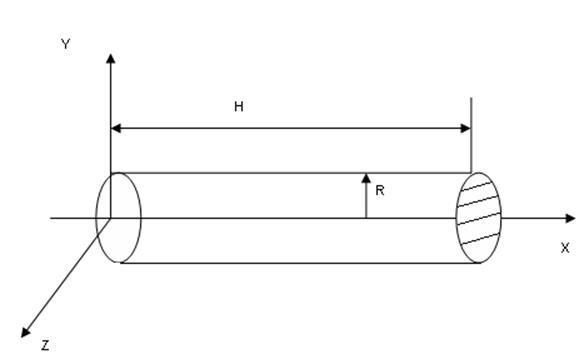
Выделенный элемент можно представить в виде диска толщенной «dx»

                            

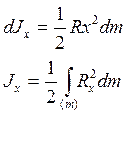
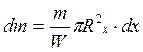
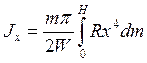      (46)

4а. Тело вращения – цилиндр.

Дано:

Rx=R,m

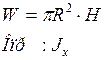
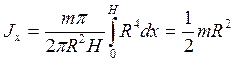
Радиус инерции а.т.т. (окружность)        

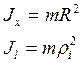
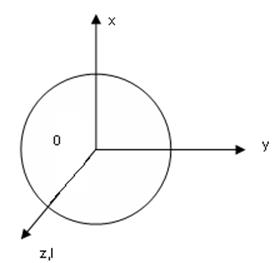
Определение:  Радиусом инерции  а.т.т. относительно оси  называется радиус такой однородной окружности, масса которой равна массе а.т.т., плоскость перпендикулярна оси  и момент инерции относительно оси равен моменту инерции а.т.т. относительно этой оси.

Теорема Гюйгенса- Штейнера.

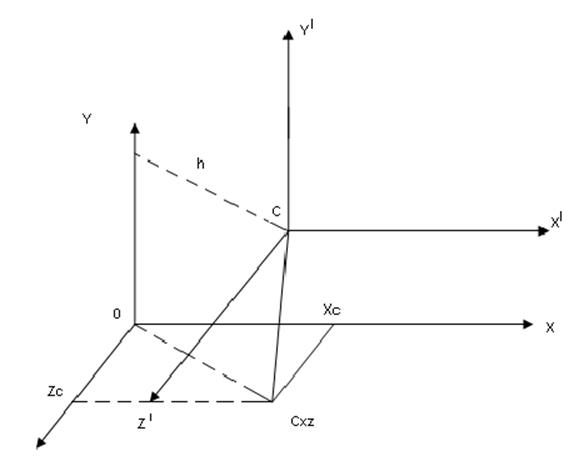
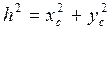
       (47)

Док-во:                                          

                  

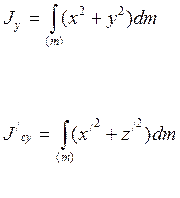
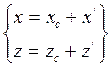
Дифференциальные уравнения движения а.т.т.

Поступательное движение а.т.т.

!!!!!!!!!!!

!!!!!!

Дано:

m,

Опр:

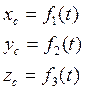
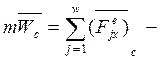Ур-е движения центра инерции а.т.т.

Проектируем на оси гл.с.к.:

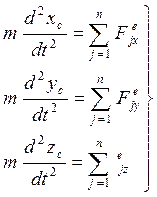(48)

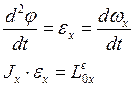
Система трех дифференциальных уравнений, хар. поступат. движение  а.т.т.

При t=0,

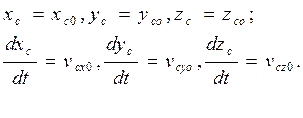
(48)-дифф-е ур-я дв-я(поступательного) а.т.т.

2)Вращательное дв-е а.т.т. вокруг(около) неподвижной оси.

Дано:

              

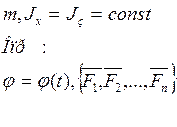
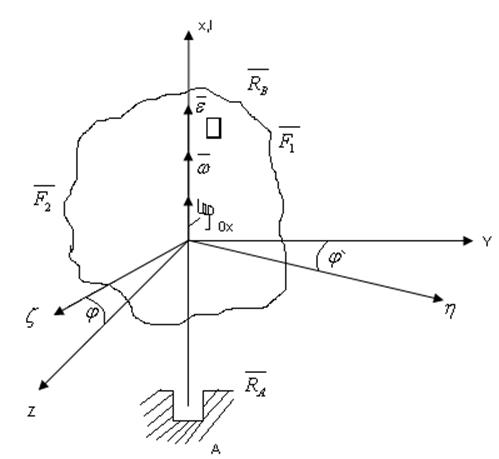
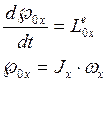
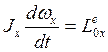      (50)- дифференциальное уравнение вращения а.т.т. около оси.

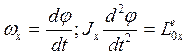(51)   (Удобно пользоваться если главный момент внешних сил является функцией «φ».)

Нач. усл.:

При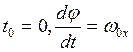

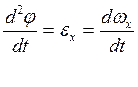
         (52)Удобно пользоваться, когда в исходной или искомой части задачи

Содержится угловое ускорение а.т.т. «ε»

Ср-ни:

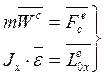Векторные уравнения поступательного и вращательного движения а.т.т.

Теорема об изменении кинетической энергии а.т.т. при его вращении около неподвижной оси.

Пусть под действием с.сил изменяются значения  до φ и  до .

            

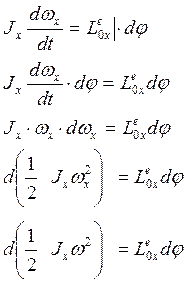
Обозначим  =     (53)

Элемент работы на элементарное угловое перемещение.

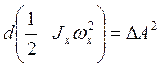,но т.к. при вращении около оси 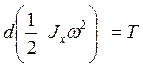 -кинетическая энергия а.т.т.

   (54)-ур-е кинетической энергии а.т.т., вращается около неподвижной в дефф-ой форме.

Интегрируя (54), получим:

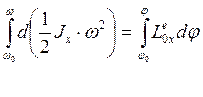
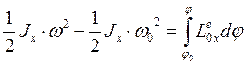     (55)-то же в интегральной форме.

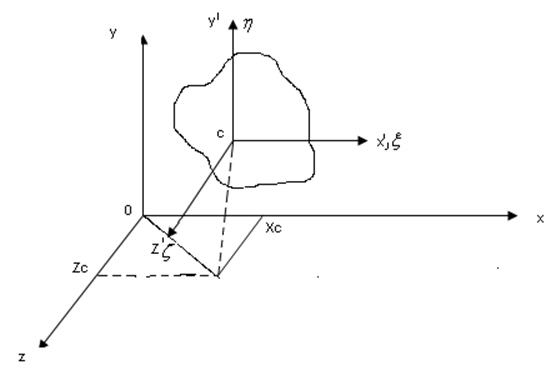
Дифференциальные уравнения плоско-параллельного движения а.т.т.

Опред. плоско-параллельного движения а.т.т.?(свойство движения:

все точки а.т.т. остаются в плоскости параллельной направляющей плоскости)

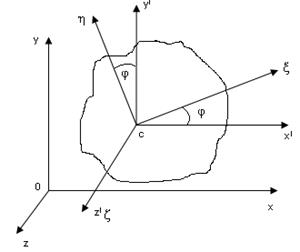
Выбираем сечение а.т.т. ,параллельное направляющей плоскости .

c,ζ,η,ξ-подчин. с.к., связанная с плоск. фигурой.

c'x'y'z'-проежутки с.к.

Oxyz-гл.с.к