Лекция №
1…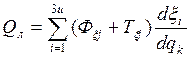 ; (k=1,2,…8)
; (k=1,2,…8)
2….![]()
qk......[м]; Qk…..[H]
qk......[рад]; Qk…..[H*м]
Определение обобщенной силы в частном случае, когда система вещественных точек находится под действием только консервативных сил (отсутствует трение).
1….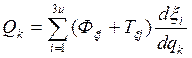 ;
(k=1,2,…8) *
;
(k=1,2,…8) *
2….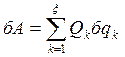 (**)
(**)
3…![]() ;
(j=1,2,…3n) из (*) следует
;
(j=1,2,…3n) из (*) следует
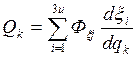 (силы
только консервативны)
(силы
только консервативны)
![]() -потенциальная функция
консервативной силы: если система сил консервативна, то можно найти
потенциальную функцию, связанную с консервативной силой.
-потенциальная функция
консервативной силы: если система сил консервативна, то можно найти
потенциальную функцию, связанную с консервативной силой.
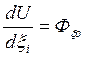 , j=(1,2,…3n)
, j=(1,2,…3n)
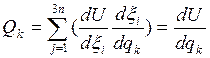 (?)
(?)
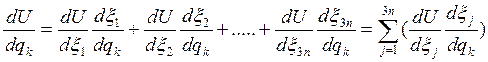 (!)
(!)
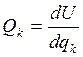 т.к. U=-П, то
т.к. U=-П, то 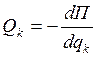 k=(1,2,…8) (68)
k=(1,2,…8) (68)
П- потенциальная энергия вещественных точек в данной точке динамического поля консервативных сил
Уравнение Лагранжа второго рода в случае, когда система вещественных точек находится под действием консервативных сил.
Рассмотрим голономную систему «к» вещественных точек
Уравнение Лагранжа для «8»-число степеней свободы системы
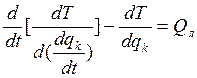 k=(1,2,….8)
k=(1,2,….8)
Т.к. система действующих сил консервативна, то:
![]()
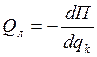 k=(1,2,….8)
k=(1,2,….8)
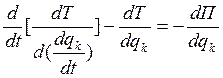 k=(1,2,….8)
k=(1,2,….8)
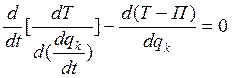 (***)
(***)
Т-П=![]() - Лагранжикан: разность
кинетической и потенциальной энергией есть функция Лагранжа
- Лагранжикан: разность
кинетической и потенциальной энергией есть функция Лагранжа
Рассмотрим: кинетическую энергию системы
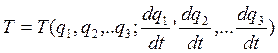 - зависит от обобщающих координат
и от обобщающих скоростей
- зависит от обобщающих координат
и от обобщающих скоростей
- потенциальная энергия системы:
П=П(q1,q2,….,q8) – зависит только от обобщающих координат
- Лагранжикан (Функция Лагранжа)
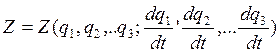 - зависит от обобщающих
координат и от обобщающих скоростей
- зависит от обобщающих
координат и от обобщающих скоростей
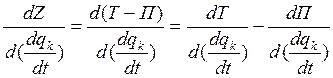 - не зависит от обобщающих
скоростей
- не зависит от обобщающих
скоростей
Тогда равенство (*) перепишем в виде:
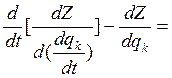 -нет решений. k=(1,2,….8)
(69)
-нет решений. k=(1,2,….8)
(69)
Система уравнений проще, т.к. уравнения однородные (правая часть = нет решений)
Пусть на две точки наложено удерживающее ограничение
f(t,x,y,z)=0, то
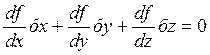
Рассмотрим понятия: возможные перемещения:
Опр. Возможным перемещением несвободной
вещественной точки отвечающим некоторому промежутку времени ![]() называется такое перемещение, которое
будет иметь эта точка при равномерном прямолинейном движении за данный
промежуток времени
называется такое перемещение, которое
будет иметь эта точка при равномерном прямолинейном движении за данный
промежуток времени ![]() без нарушения характера
ограничения которым подчиняются её движения.
без нарушения характера
ограничения которым подчиняются её движения.
Возможное перемещение точки обозначается дифференциалами координат:
![]() dx
dx
dr dy
dz
Условия которые налагают ограничения на возможные перемещения точки будут иметь следующий вид:
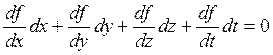
Пример: см. математический маятник. Возможное перемещение не совпадает с виртуальным
Совпадает, если l(t)=const x2+y2=l2(t)
Различие виртуальных и возможных перемещений:
Начало возможных перемещений.
При возможном перемещении несвободной системы вещественных точек. Находящихся в состоянии неподвижности относительно выбранной системы отсчета, сумма работ всех сил, не зависящих от ограничивающих тел и всех сил трения, действует на все точки данной системы, = нулю (0), при условии, что на протяжении всего возможного перемещения эти силы остаются такими, какими они были до перемещения.
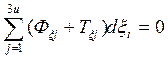 (70)
(70)
N.в: начало возможных перемещений сформулировано для случая, когда система находится в неподвижном состоянии
Де’Аламбером были введены фиктивные силы инерции (силы Де’Аламбера)
![]() (71)
(71)
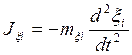 (71)’
(71)’
Начало Де’Аламбера.
Если к действительным силам, действующим на несвободную систему вещественных точек, прибавить фиктивные силы инерции, то систему вещественных точек можно рассматривать находящейся в квазистатическом состоянии и применять к ней все теоремы и начало статики, том числе и начало возможных перемещений.
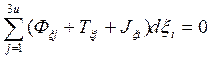 (72)
уравнение Де’Аламбера-Лагранжа
(72)
уравнение Де’Аламбера-Лагранжа
Этот прием Де’Аламбера-Лагранжа является теоретической основой метода кинетостатики
![]()
![]()
![]()
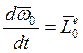
![]()
![]()
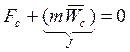
![]()
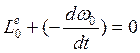
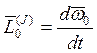
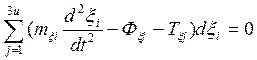 (общее
уравнение динамики для не изменяющихся ограничений)
(общее
уравнение динамики для не изменяющихся ограничений)
Начало верхних перемещений и уравнение Де’Аламбера-Лагранжа получены для системы, которые подчиняются конечным и неизменяемым ограничением, чтобы распространить уравнение Д-Л по изменению и дифференцированию ограничения, необходимо в уравнении (72) возможные перемещения заменить на виртуальные..
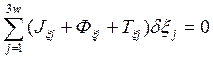 (73)
(73)
Малые колебания систем вещественных точек.
Известно, что система вещественных точек может совершать малые колебания около положения устойчивого равновесия системы. (В равновесии находится система сил, действующих на систему вещественных точек)
Рассмотрим положения равновесия:
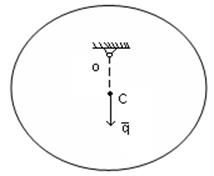
1) устойчивое
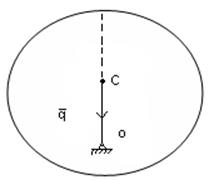
2) неустойчивое
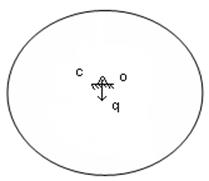
3) безразличное
Пример: физический маятник, который находится под действием силы тяжести.
1) 2) 3)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.