Уравнение Лагранжа второго рода в случае, когда система вещественных точек находится под действием консервативных сил, страница 2

Q_k=0 (k=1,2,3……..8)

                                       

                                    Q=0

                                                  

                           

                                    

Определение устойчивого и неустойчивого положения равновесия дал русский ученый Ляпунов А. И.

Пусть обобщенные координаты системы    _t=0 в начальный момент времени (q_k)_рв – в момент равновесия системы.

Определение: Положение систем вещественных точек, отвечающее равновесию приложенных к  ней сил, называются устойчивым, если для  положительного числа . Можно найти такое положительное число «» для которого имеет место неравенство вида

 

      

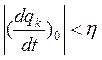
И в момент времени «t» будут иметь место неравенства вида

 для всех (k=1,2,3….8)

Если же: Положение систем вещественных точек, отвечающее равновесию приложенных к  ней сил, называются  неустойчивым, если для некоторого числа  можно указать такое число , для которого выполняются неравенство

 

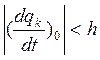
И в некоторый момент времени «t» имеет место хотя бы одно равентсво вида

 для всех (k=1,2,3….8)

Принцип устойчивости равновесия (достаточный),  сформулирован теоремой Лагранжа-Дирихле. Для того чтобы положения голономной системы вещественных точек. Отвечающее равновесию приложенных к ней консервативных сил было устойчивым, достаточно. Чтобы в этом положении потенциальная энергия системы имела min значение.

(П)_рв=П_min

(q_k)_рв=0  (к=1,2,…..8)

(П)_рв=П_min=0

N.в.! Необходимого признака устойчивости положения равновесия не существует, но имеются теоремы Ляпунова А.И

Теоремы Ляпунова А.И о неустойчивости положения равновесия.

Положение голономной системы вещественных точек. Отвечающее равновесию приложенной к ней системы сил, будет безусловно неустойчивым, если:

1. В указанном положении отсутствует min потенциальной энергии, определяемой членами второго порядка малости этой функции при разложении в ряд Тейлора около положения равновесия
2. Наличие max потенциальной энергии определяется членами наименее высоко порядка малости не обращающихся в 0 в разложении этой функции в ряд Тейлора около положения равновесия.

Разложение потенциальной энергии в ряд около положения рвновесия.

будем сохранять                           не выше 2ого порядка малости для получения линейной системы:

1ое слагаемое =0, если система находиться  равновесии, то 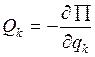=0, тогда потенциальная энергия получается в виде :

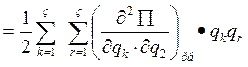
Обозначим: 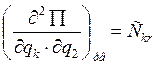- коэффициент  квазиупрогости, постоянные могут быть «+» и  «-».

Например: 

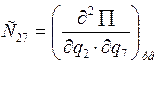-вторая произв. от потенц. энергии системы 2ой и 7ой коорд.

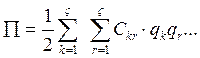 (74) –Потенциальная энергия системы в случае малых колебаний.

Пусть система имеет одну степень свободы :ζ=1

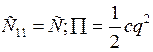     (75)

В случае устойчивого положения равновесия С>0

Пусть:ζ=2, 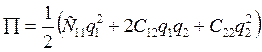        (76)

Равенство (74) показывает ,что в случае малых колебаний потенциальная энергия является однородной положительной  квадратичной формой обобщенных координат.

Критерий Сильвестра

условия при которых однородная форма является «+»-ой в квадратичной формой (в матем.)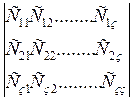

Необходимо, что бы все миноры данного определителя были положительными.

Например:

Если система имеет «ζ» степеней свободы , то все «ζ» миноров должны быть положительными.

1)

2)

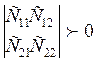
3)

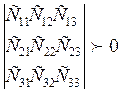
При ζ=1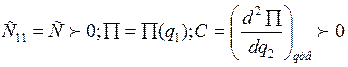

при консервативных силах :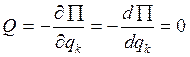

См.пример: физический маятник

 

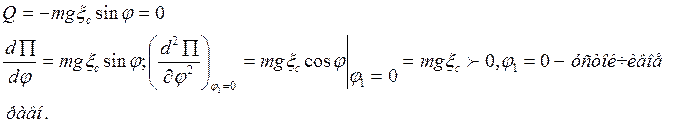
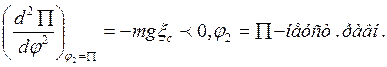
Кинетическая энергия системы вещ-х точек в случае малых колебаний.

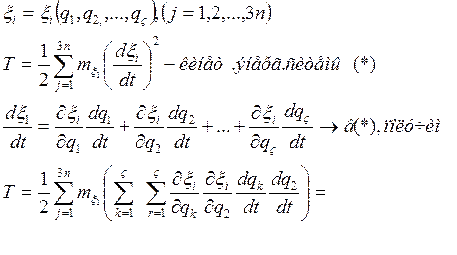
поменяем местами порядок суммирования по j и по k,r получим:

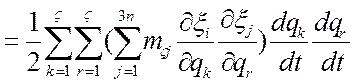
Обозначим:

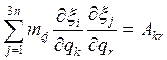-коэфицент квазитивности системы

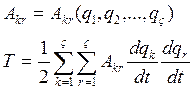
Функцию разложим в ряд Тейлора около положение равновесия сист.

 

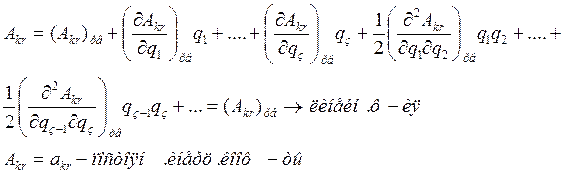
В случае малых колебаний системы вещественных точек кинетическая энергия выражается следующей однородной положительной квадратичной формой обобщ-х скоростей

                         

                         

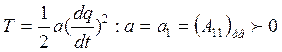
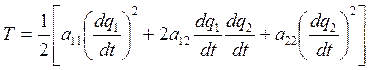
инерционные коэфиценты должны удовлетворять след-м условием:

Классификация сил, действующих на систему вещ-х точек.

1)консервативные силы

2)неконсервативные силы

3)возмущающие силы

обобщенная сила, соотв-щая консервативным силам;

 обобщенная сила, соотв-щая  неконсервативным силам;

- обобщенная сила, соотв-щая  возмущающимся силам.

к - обобщенная сила , соотв. обобщ. к-те    

1. 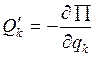 (для консервативных сил).

2. Определение обобщенных сил, соответствующих силам неконсервативным (силы трения)

(силы вязкого трения , пропрцион-е 1 степени скорости и турбулейного трения ~2 степени скор-и)

Ур-я, описывающие такое движение (с трением) –нелинейные дифф-е ур-я

 -сила сопратевления движению

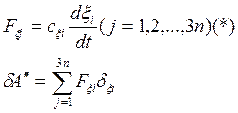
Перенесем (*)=>

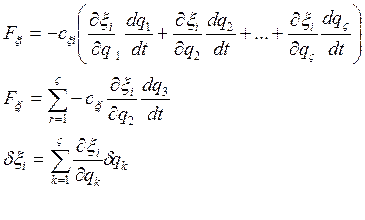
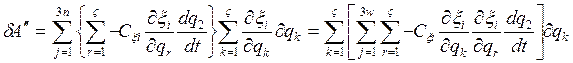
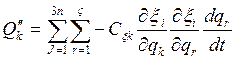-Обобщ. сила ,соотв-я неконсервативным силам, действующим на сист. точек и соотв-я обобщ-й координате qk

Введем в рассмотрение след. ф-ию:

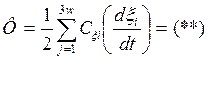
Ф- диссипативная ф-ия, ф-ия рассеяния энергии, ф-ия Гелея.

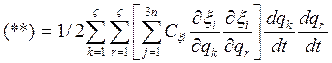
Можно заметить, что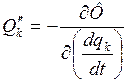

Обозначим:

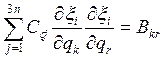
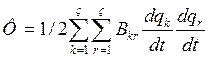
В случае малых колебаний сист., разлагая в ряд Тейлера около положения равновесия и ограничиваясь первыми жел., получим

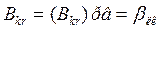
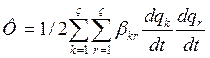-диссипативная  ф-ия –однородная, положит. квадратичная ф-ия обобщ-х  скоростей.

Можно доказать, что диссипативная функция называется функцией рассеяния, характ-ей убывание полной механической энергии системы.

 

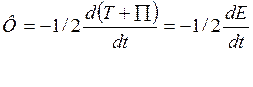
3.Возмущающие силы

(2 вар)

-обобщ. силы явл-ся переодическими функциями;

-обобщ. силы явл-ся произвольн. ф-цией времени t

Дифф-е ур-е колебаний системы получаются из ур-й Лагранжа.

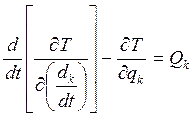       (k=1,2,3…)