5.2. Составление системы уравнений.
Запишем систему уравнений (1.2.4) для рассматриваемой цепи:
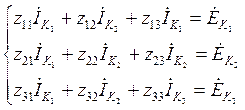 , в
матричной форме:
, в
матричной форме: ![]() (5.2)
(5.2)
5.3. Определение матрицы коэффициентов ![]() .
.
Определим коэффициенты ![]() в соответствии с п. 1.2.4:
в соответствии с п. 1.2.4:
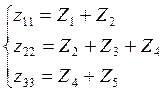 ,
, 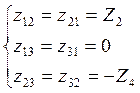 и запишем их в матричной форме:
и запишем их в матричной форме:
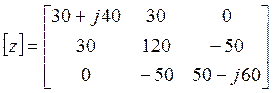 (5.3)
(5.3)
5.4. Определение вектора свободных членов ![]() .
.
Определим коэффициенты ![]() в соответствии с п. 1.2.4:
в соответствии с п. 1.2.4:
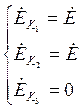 , в
матричной форме:
, в
матричной форме: 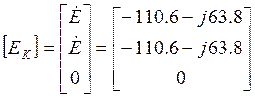 (5.4)
(5.4)
5.5. Нахождение вектора контурных токов ![]() и токов в ветвях
и токов в ветвях ![]() .
.
Подставим найденные значения (5.3) и (5.4) в уравнение (5.2):
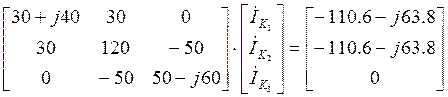 (5.5)
(5.5)
Решим матричное уравнение (5.5) с помощью ЭВМ:
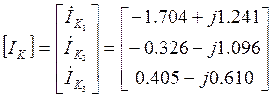
Подставив полученные значения контурных токов найдем искомые токи в ветвях:
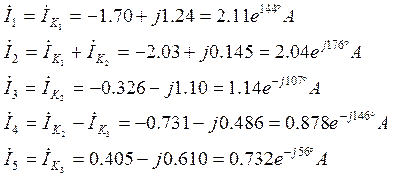
Полученные значения токов совпадают со значениями, полученными при расчете методом эквивалентных преобразований в п. 3.2.
 6. Расчет методом узловых потенциалов.
6. Расчет методом узловых потенциалов.
Для расчета методом узловых
потенциалов (п. 1.2.5) необходимо ввести новые переменные – узловые потенциалы,
пронумеровать все узлы цепи и принять потенциал одного из узлов равным нулю.
Принимаем ![]() .
.
Также для составления уравнений
необходимо вычислить комплексы проводимостей всех ветвей цепи: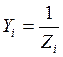 .
.
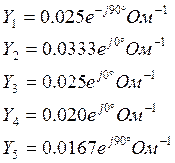
6.1. Выражение токов в ветвях через узловые потенциалы.
Токи в ветвях определяются разностью потенциалов на между конечным и начальным узлом ветви, причем токи текут из области с более высоким потенциалом в область с более низким потенциалом. На основании этого можно выразить все токи через потенциалы узлов:
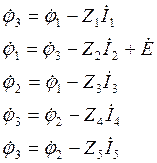
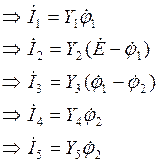 (6.1)
(6.1)
6.2. Составление системы уравнений.
Запишем систему уравнений (1.2.5) для рассматриваемой цепи:
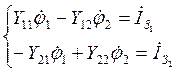 , в
матричной форме:
, в
матричной форме: ![]() (6.2)
(6.2)
6.3. Определение матрицы коэффициентов ![]() .
.
Определим коэффициенты ![]() в соответствии с п. 1.2.5:
в соответствии с п. 1.2.5:
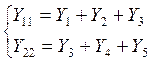 ,
, ![]() и запишем их в матричной форме:
и запишем их в матричной форме:
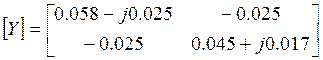 (6.3)
(6.3)
6.4. Определение вектора свободных членов ![]() .
.
Определим коэффициенты ![]() в соответствии с п. 1.2.5:
в соответствии с п. 1.2.5:
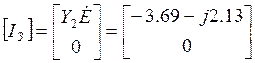 (6.4)
(6.4)
6.5. Нахождение вектора узловых потенциалов ![]() и токов в ветвях
и токов в ветвях ![]() .
.
Подставим найденные значения (6.3) и (6.4) в уравнение (6.2):
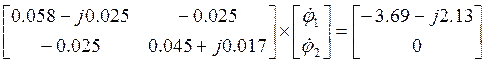 (6.5)
(6.5)
Решим матричное уравнение (6.5) с помощью ЭВМ:
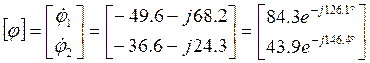
Подставив полученные значения узловых потенциалов найдем искомые токи в ветвях:
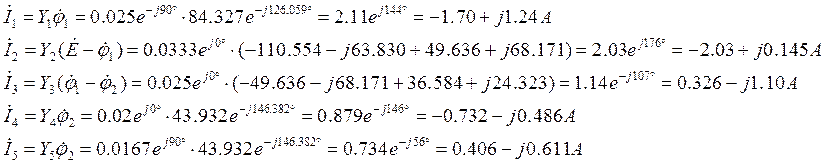
Полученные значения токов совпадают со значениями, полученными при расчете методом эквивалентных преобразований в п. 3.2.
7. Выводы.
В проделанной работе я научился расчитывать установившиеся процессы в линейной электрической цепи синусоидального тока различными методами, оценил их достоинства и недостатки, а также специфику их применения. В данной работе все рассмотренные методы применимы и дают одинаковые результаты с высокой степенью точности. Полученные в результате расчета токи и напряжения приведены в таблице 1.
Также я оценил баланс мощностей для исследуемой цепи, полученные расхождения оказались в пределах погрешности вычислений.
Определил показания измерительных приборов, включенных в цепь – амперметр, вольтметр и ваттметр:
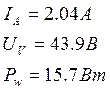
Также я научился строить векторные диаграммы токов и напряжений и проверять по ним выполнение законов Кирхгофа.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.