Расчет установившихся процессов в линейной электрической цепи синусоидального тока, страница 3

Метод контурных токов позволяет сократить число совместно решаемых уравнений за счет введения новых переменных – контурных токов. Контурный ток – расчетный ток, считаем, что в каждом контуре протекает один ток.

Для расчета методом контурных токов необходимо составить и решить систему из n=p-(q-1) уравнений:

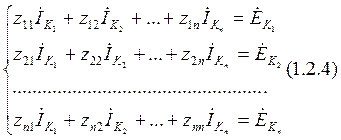Расчет матрицы коэффициентов  производится следующим образом: элементы главной диагонали вычисляются как собственные сопротивления соответствующих контуров. Остальные элементы. вычисляются как взаимные сопротивления контуров, т.е. суммарное сопротивление ветви, являющейся общей для рассматриваемых контуров, причем сопротивление берется с положительным знаком, если направления контурных токов в рассматриваемой ветви совпадают.

Вектор свободных членов  - контурные ЭДС определяются как алгебраическая сумма комплексов ЭДС, входящих в контур. ЭДС входит в сумму с положительным знаком, если ее направление совпадает с выбранным направлением контурного тока.

После решения системы уравнений и нахождения контурных токов, необходимо выразить токи в ветвях через контурные токи. Ток в ветви равен алгебраической сумме контурных токов, соответствующих контурам, через которые протекает рассматриваемый ток. Если направление тока совпадает с направлением контурного тока, то контурный ток берется с положительным знаком.

1.2.5. Метод узловых потенциалов.

Метод узловых потенциалов позволяет сократить число совместно решаемых уравнений за счет введения новых переменных – узловых потенциалов. Так как токи в ветвях определяются разностью потенциалов, то потенциал одного из узлов можно принять равным нулю.

Для расчета методом узловых потенциалов необходимо составить и решить систему из n=(q-1) уравнений:

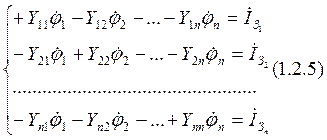В данной системе уравнений коэффициенты, стоящие на главной диагонали, берутся с положительным знаком, остальные – с отрицательным.

В матрице коэффициентов  коэффициенты, стоящие на главной диагонали, определяются как сумма проводимостей всех ветвей, сходящихся в узле. Остальные элементы определяются как сумма проводимостей всех ветвей, связывающих непосредственно соответствующие узлы.

Вектор свободных членов  - задающие токи определяются как алгебраическая сумма произведений проводимостей соответствующих ветвей, сходящихся в узле, на ЭДС, действующие в ветви, причем слагаемое берется с положительным знаком, если соответствующая ЭДС направлена к узлу: .

После решения системы уравнений и нахождения узловых потенциалов, необходимо выразить токи в ветвях через узловые потенциалы. Для этого выражаются потенциалы конечных узлов ветви, содержащей рассматриваемый ток, через начальные потенциалы.

2. Составление системы уравнений по законам Кирхгофа.

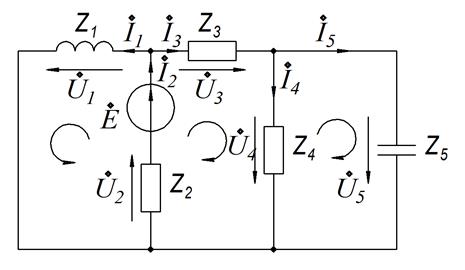
В цепи, приведенной на рисунке, зададимся направлением токов, напряжений и направлением обхода контуров.

Цепь содержит 5 ветвей и 3 узла, то есть необходимо составить 5 уравнений по законам Кирхгофа – два уравнения по первому закону Кирхгофа (1.1.1) и три уравнения по второму закону Кирхгофа (1.1.2).

p = 5;  q = 3, общее число уравнений – n = p – (q – 1).

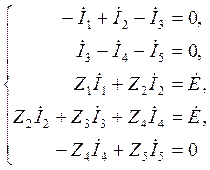                                                                                                                     (2.1)

В матричной форме уравнение (2.1) будет иметь вид: .

Перепишем его с числовыми значениями:

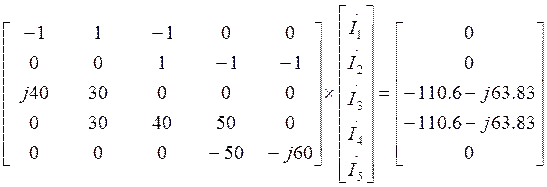                                                                                                                     (2.2)

Решая матричное уравнение (2.1) с помощью ЭВМ, получим:

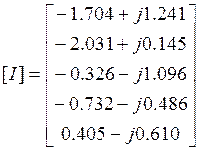
Представим токи в алгебраической и показательной форме:

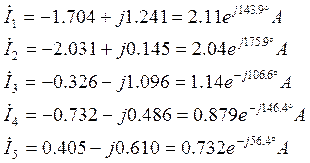
Рассчитаем теперь напряжения по формуле (1.1.3):

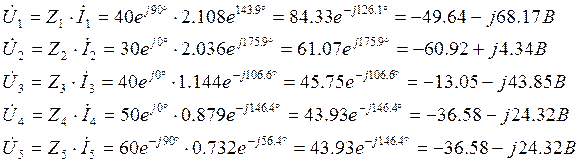
3. Расчет цепи методом эквивалентных преобразований.

3.1. Расчет комплекса полного входного сопротивления.

1).Первая схема замещения.

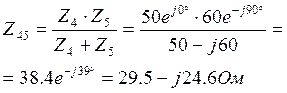
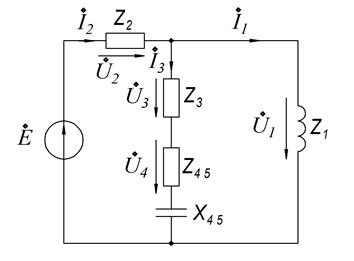Сопротивление  имеет активно-емкостной характер.

2).Вторая схема замещения.

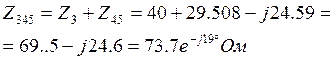
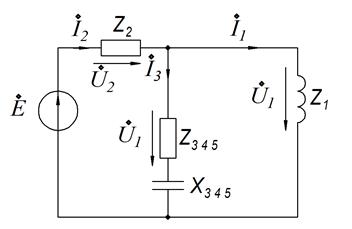Сопротивление  имеет активно-емкостной характер.

3). Третья схема замещения.

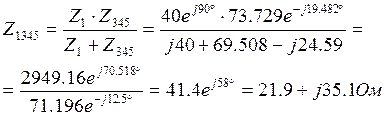
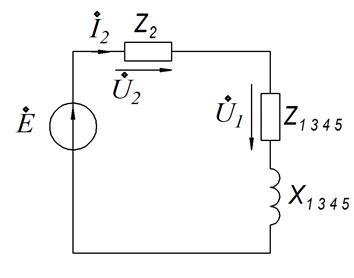Сопротивление  имеет активно-индуктивный характер.