где ![]() -
комплексы действующих значений напряжения и тока на участке цепи
соответственно, а Z – комплекс полного сопротивления
участка цепи:
-
комплексы действующих значений напряжения и тока на участке цепи
соответственно, а Z – комплекс полного сопротивления
участка цепи:
![]()
Также закон Ома можно записать, используя комплекс полной проводимости участка цепи:
![]() , где
, где 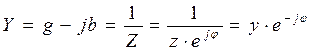 -
комплекс полной проводимости.
-
комплекс полной проводимости.
Для отдельных идеальных элементов цепи закон Ома можно записать с учетом комплекса сопротивления элемента:
для резистивного элемента: ![]()
для индуктивного элемента: ![]()
для емкостного элемента: 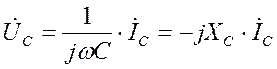
1.1.4. Расчет мощностей комплексным методом.
Комплекс полной мощности равен произведению комплекса действующего значения напряжения на сопряженный комплекс действующего значения тока:
![]() , где
, где 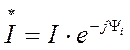 -
сопряженный комплекс действующего значения тока
-
сопряженный комплекс действующего значения тока
Тогда комплекс полной мощности можно представить в следующем виде:
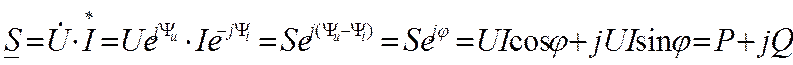
где ![]() - угол
сдвига фаз между напряжением и током;
- угол
сдвига фаз между напряжением и током;
S – полная мощность
![]() -
активная мощность
-
активная мощность
![]() -
реактивная мощность
-
реактивная мощность
1.1.5. Баланс мощностей.
Проверка баланса мощностей проводится в соответствии с уравнением
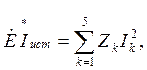 (1.1.5)
(1.1.5)
где ![]() –
сопряженный комплекс тока ветви, в которую включен источник,
–
сопряженный комплекс тока ветви, в которую включен источник, ![]() - комплексное напряжение источника,
- комплексное напряжение источника, ![]() – комплекс сопротивления и действующий ток
ветви
– комплекс сопротивления и действующий ток
ветви ![]() .
.
1.2. Методы расчета установившегося режима в электрических цепях синусоидального тока.
1.2.1. Расчет по законам Кирхгофа.
Метод расчета по законам Кирхгофа (1.1.1–1.1.2) является простым и универсальным методом расчета электрических цепей. Он позволяет рассчитывать как установившиеся, так и переходные режимы, как в линейных, так и в нелинейных цепях, как в цепях с сосредоточенными параметрами, так и в цепях с распределенными параметрами.
Для расчета этим методом необходимо составить систему уравнений с неизвестными токами. По первому закону Кирхгофа составляется (q-1) уравнений, где q – количество узлов цепи. По второму закону составляют (p-(q-1)) уравнений, где p – количество ветвей в цепи. В итоге получится система из p уравнений, которая разрешается относительно токов.
1.2.2. Метод эквивалентных преобразований.
Суть метода заключается в упрощении исходной цепи путем замены нескольких элементов одним эквивалентным. Преобразование называют эквивалентным, если напряжение, ток и угол сдвига фаз между напряжением и током на участке цепи, не затронутом преобразованием, остаются неизменными.
Метод применяют:
1). для упрощения цепи;
2). в случае действия в цепи одного источника, для расчета токов и напряжений.
Основные расчетные формулы метода основаны на вычислении эквивалентного полного сопротивления нескольких элементов, включенных последовательно или параллельно:
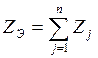 - полное эквивалентное
сопротивление при последовательном соединении
- полное эквивалентное
сопротивление при последовательном соединении
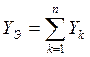 - полная эквивалентная
проводимость при параллельном соединении.
- полная эквивалентная
проводимость при параллельном соединении.
1.2.3. Метод эквивалентного генератора.
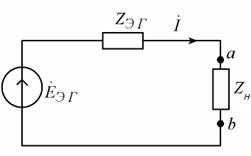 Метод применяют в тех
случаях, когда сложная линейная цепь работает на переменную нагрузку. Суть
метода заключается в замене части сложной линейной цепи (за исключением цепи,
содержащей нагрузку) эквивалентным генератором, т.е. метод позволяет сложную
цепь свести к последовательному соединению эквивалентного генератора с
параметрами
Метод применяют в тех
случаях, когда сложная линейная цепь работает на переменную нагрузку. Суть
метода заключается в замене части сложной линейной цепи (за исключением цепи,
содержащей нагрузку) эквивалентным генератором, т.е. метод позволяет сложную
цепь свести к последовательному соединению эквивалентного генератора с
параметрами ![]() ,
,![]() и сопротивлению
нагрузки
и сопротивлению
нагрузки ![]() .
.
Тогда ток в нагрузке будет определяться формулой:
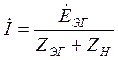 . (1.2.3.1)
. (1.2.3.1)
Для расчета параметров
эквивалентного генератора ![]() ,
,![]() необходимо
разомкнуть ветвь, содержащую нагрузку (ветвь ab). Тогда
в соответствии с теоремой об эквивалентном генераторе
необходимо
разомкнуть ветвь, содержащую нагрузку (ветвь ab). Тогда
в соответствии с теоремой об эквивалентном генераторе ![]() равно
напряжению на зажимах разомкнутой цепи ab в режиме
холостого хода:
равно
напряжению на зажимах разомкнутой цепи ab в режиме
холостого хода:
![]() . (1.2.3.2)
. (1.2.3.2)
Эквивалентное полное сопротивление генератора вычисляется как полное сопротивление участка цепи ab.
1.2.4. Метод контурных токов.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.