4).Конечная схема замещения.
![]()
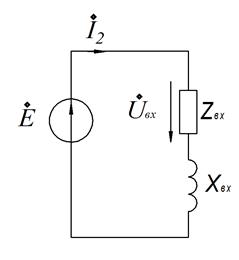 Сопротивление
Сопротивление
![]() имеет активно-индуктивный характер.
имеет активно-индуктивный характер.
3.2. Расчет токов и напряжений.
Ток ![]() в
конечной схеме замещения определяется формулой:
в
конечной схеме замещения определяется формулой: 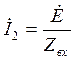
Остальные токи и напряжения определяются из закона Ома (1.1.3).
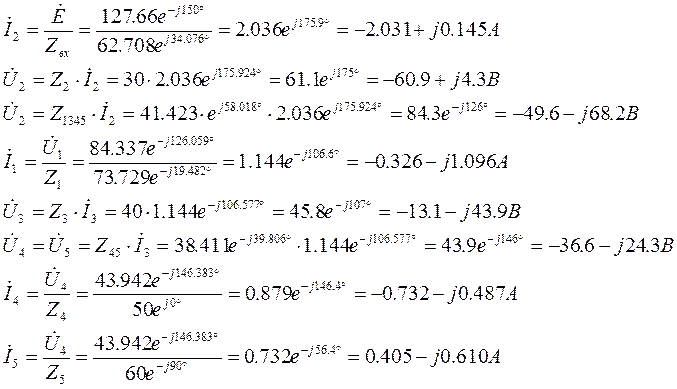
Представим полученные значения в виде таблицы:
Таблица 3.2.1.
|
Величина |
Алгебраическая форма |
Показательная форма |
Мгновенные значения ( |
|
|
|
А |
|
|
|
|
|
А |
|
|
|
|
|
А |
|
|
|
|
|
А |
|
|
|
|
|
А |
|
|
|
|
|
В |
|
|
|
|
|
В |
|
|
|
|
|
В |
|
|
|
|
|
В |
|
|
|
|
|
В |
|
|
|
3.3. Баланс мощностей.
Проверку баланса мощностей будем проводить на основе формулы (1.1.5):
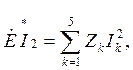
где ![]() – сопряженный комплекс тока
ветви, в которую включен источник,
– сопряженный комплекс тока
ветви, в которую включен источник, ![]() - комплексное
напряжение источника,
- комплексное
напряжение источника, ![]() – комплекс сопротивления и
действующий ток ветви
– комплекс сопротивления и
действующий ток ветви ![]() .
.
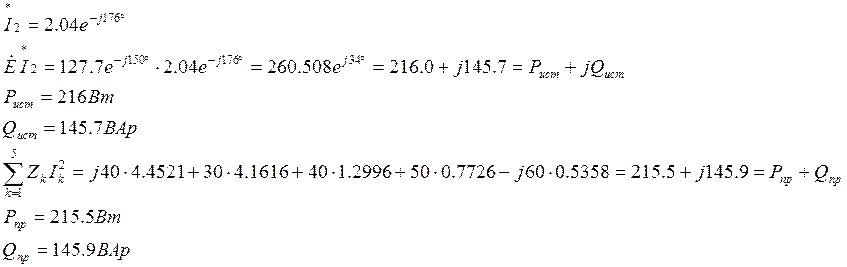
Проводим оценку баланса по формулам
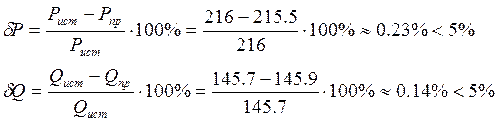
Полученное расхождение находится в пределах погрешности вычислений.
3.4. Определение показаний измерительных приборов.
Амперметр показывает действующее значение тока:
![]() .
.
Вольтметр показывает действующее напряжения:
![]() .
.
Показание ваттметра определяется произведением действующих значений измеряемого напряжения и измеряемого тока, умноженным на косинус сдвига фаз между ними:
![]() .
.
3.5. Построение векторной диаграммы токов и напряжений.
Для построения векторной диаграммы воспользуемся алгебраической формой записи комплексов токов и напряжений. Проверку выполнения законов Кирхгофа – можно провести пунктирными линиями – по правилу сложения векторов.
Масштаб диаграммы по токам равен 0,2 А/см, по напряжениям 20 В/см.
3.6. Определение влияния изменения частоты в n раз на величину сопротивления каждого сопротивления.
Обозначим измененную частоту: ![]() .
.
Считаем, что все элементы цепи – идеальные, тогда для активных элементов сопротивление не изменится, для индуктивных и емкостных будет определяться соответствующими формулами:
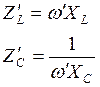
В соответствии с этим получим:
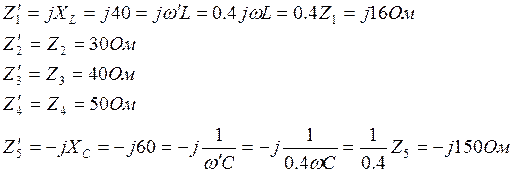
4. Расчет тока в ветви 5 методом эквивалентного генератора.
4.1. Определение ЭДС эквивалентного генератора.
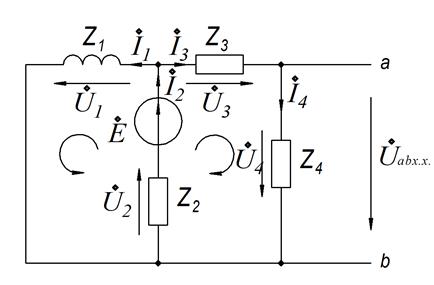 Для нахождения тока
Для нахождения тока ![]() размыкаем ветвь, по которой течет этот ток
– ветвь ab. Тогда по формуле (1.2.3.2) ЭДС
эквивалентного генератора будет равна:
размыкаем ветвь, по которой течет этот ток
– ветвь ab. Тогда по формуле (1.2.3.2) ЭДС
эквивалентного генератора будет равна:
![]()
Для нахождения ![]() составим систему уравнений по законам
Кирхгофа, решим ее относительно токов и найдем
составим систему уравнений по законам
Кирхгофа, решим ее относительно токов и найдем ![]()
Для полученной цепи p=3, q=2, значит необходимо составить 1 уравнение по первому закону Кирхгофа (1.1.1) и 2 уравнения по второму закону Кирхгофа (1.1.2):
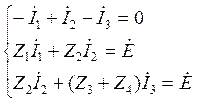 , в
матричной форме:
, в
матричной форме: 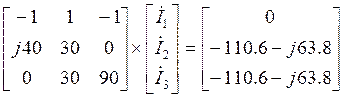
Решив полученное матричное уравнение с помощью ЭВМ, получим:
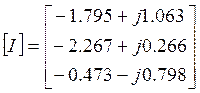
Тогда ЭДС эквивалентного генератора будет равно:
![]()
4.2. Определение комплекса внутреннего сопротивления эквивалентного генератора.
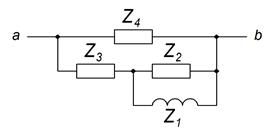 Для нахождения комплекса внутреннего сопротивления
эквивалентного генератора
Для нахождения комплекса внутреннего сопротивления
эквивалентного генератора ![]() воспользуемся
эквивалентной схемой. Тогда внутреннее сопротивление эквивалентного генератора
будет равно полному сопротивлению ветви ab.
воспользуемся
эквивалентной схемой. Тогда внутреннее сопротивление эквивалентного генератора
будет равно полному сопротивлению ветви ab.
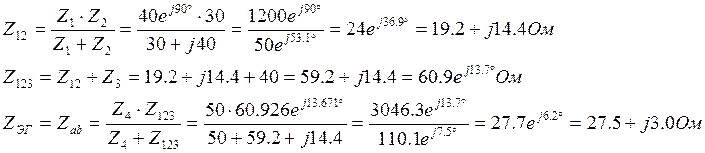
4.3. Определение тока в нагрузке.
Найдем искомый ток в нагрузке ![]() по формуле (1.2.3.1):
по формуле (1.2.3.1):
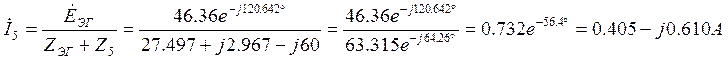
Полученное значение для ![]() совпадает со значением, полученном при расчете
токов методом эквивалентных преобразований в п. 3.2.
совпадает со значением, полученном при расчете
токов методом эквивалентных преобразований в п. 3.2.
5. Расчет методом контурных токов.
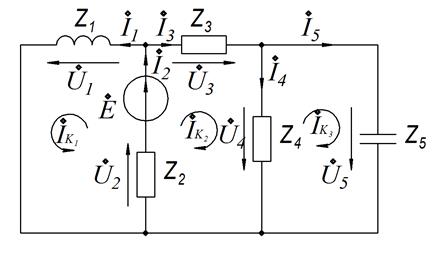 Для расчета методом контурных
токов (п. 1.2.4) необходимо ввести новые расчетные переменные – контурные токи,
и задаться их направлением в каждом независимом контуре.
Для расчета методом контурных
токов (п. 1.2.4) необходимо ввести новые расчетные переменные – контурные токи,
и задаться их направлением в каждом независимом контуре.
5.1. Выражение токов в ветвях через контурные токи.
Выразим токи в ветвях через соответствующие контурные токи:
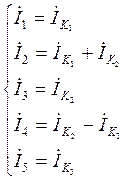 (5.1)
(5.1)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.