ЦНИИ «Электроприбор»
Преподаватель Лопарев А.В.
Рейтинг за работу
Отчет
По лабораторной работе
«Изучение распределений случайных величин»
Вариант задания: экспоненциальное распределение, параметр=2.
Работу выполнил
Студент гр. 1421 Боровков М. Г.
Санкт - Петербург
2008г.
1.1. Вычислить математическое ожидание и дисперсию при заданных параметрах.
[m,v]=expstat(2)
m=2, v=4
1.2. С использованием Matlab на одном и том же рисунке постройте графики ф.п.р.в. при заданных параметрах и при их значениях, уменьшенных в два раза.
Первый график:
x=0:0.01:20;
y=exppdf(x,2);
plot(x,y);
hold on
Второй график на том же рисунке:
y=exppdf(x,1);
plot(x,y);
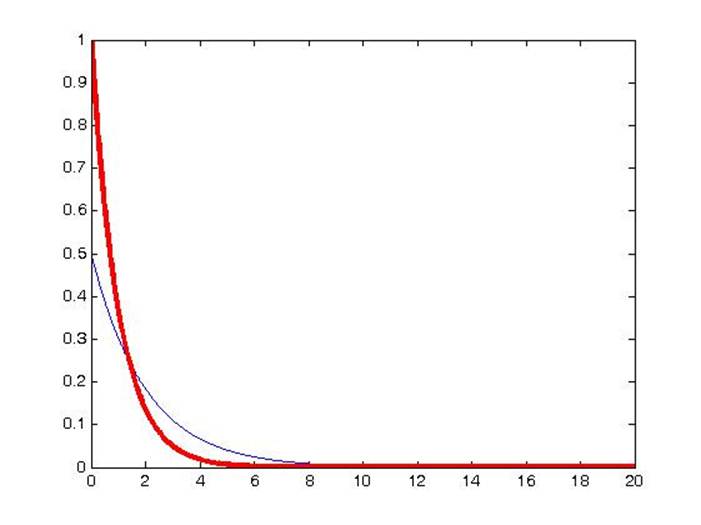
График, построенный тонкой линией – для параметра 2, жирной линией – для уменьшенного в 2 раза. При уменьшении параметра в 2 раза график, начальное значение в 2 раза увеличивается, также увеличивается крутизна падения экспоненты. Поскольку параметр в нашем случае равен мат. Ожиданию, то только такое изменение графика могло сохранить площадь под ним неизменной.
1.3 С использованием соответствующих m- функций Matlab получите 200 реализаций случайных величин, вычислите выборочные значения математического ожидания, дисперсии и медианы. Повторите эти вычисления при числе реализаций, равном 20000, постройте гистограмму. Поясните полученные результаты.
R=exprnd(2,200,1)
R1=exprnd(2,20000,1)
mean(R)= 1.9794
mean(R1)= 2.0066
median(R)= 1.2362
median(R1)= 1.3797
var(R)= 4.6666
var(R1)= 4.1728
Видно, что при большем числе элементов выборки моментные характеристики ближе к теоретическим.
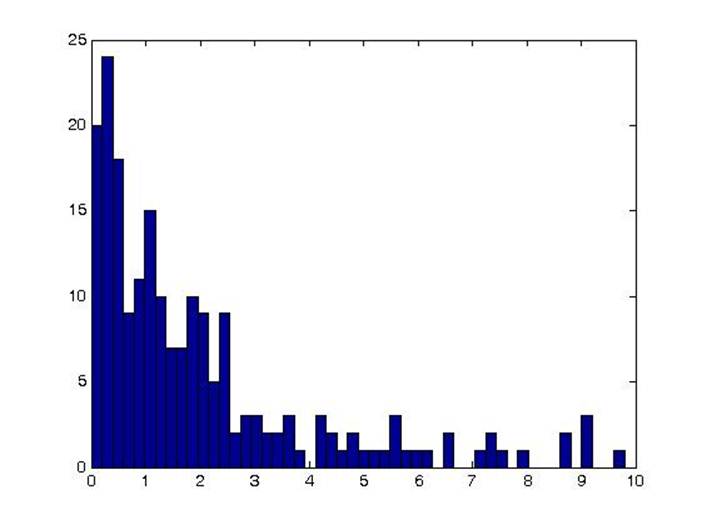
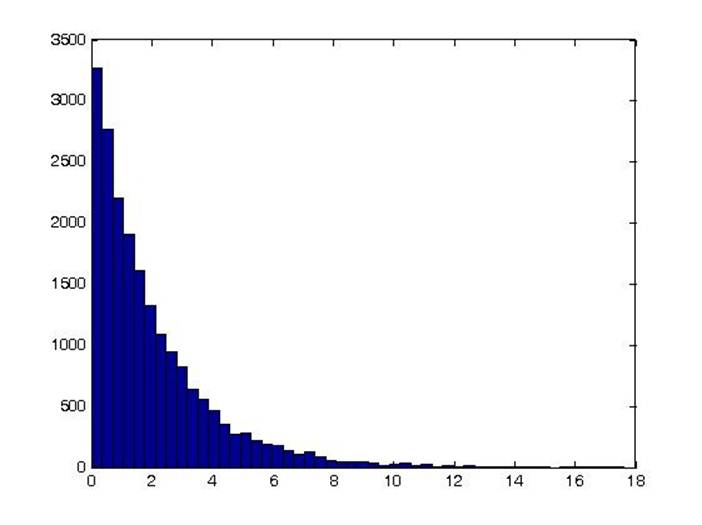
При большем числе элементов выборки гистограмма получается более гладкой и похожей на теоретический вид распределения.
2.1. Запишите выражение для ф.п.р.в.
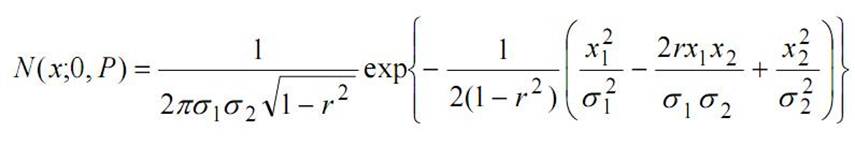
2.2 Найдите параметры среднеквадратического эллипса ошибок. Вариант 1.
σ1=1; σ2=2; r=0.5
2.3 С помощью Matlab (так как это описано в приложении) постройте график этой двумерной функции с соответствующими ему изолиниями.
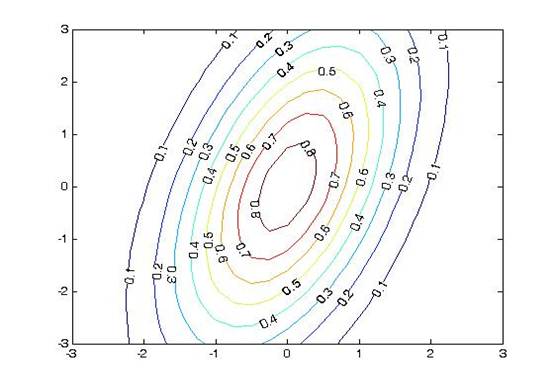
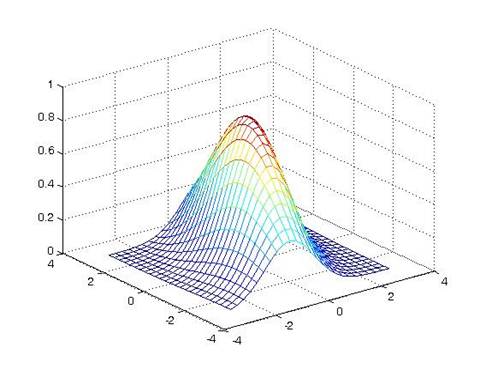 Трехмерный график ф.п.р.в. Видно, что вдоль одной из осей
дисперсия существенно больше, чем вдоль другой.
Трехмерный график ф.п.р.в. Видно, что вдоль одной из осей
дисперсия существенно больше, чем вдоль другой.
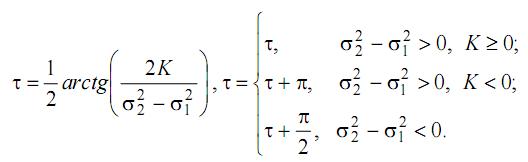
K=1, τ=16,8450
Видно, что наши эллипсы повернуты относительно вертикальной оси примерно на этот угол, т.е. получили адекватное значение.
2.4 Теперь определяем проекцию вектора на направление τ*=300
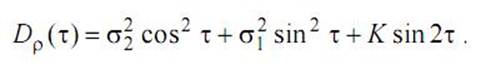
D= 4.1122
Получили дисперсию проекции.
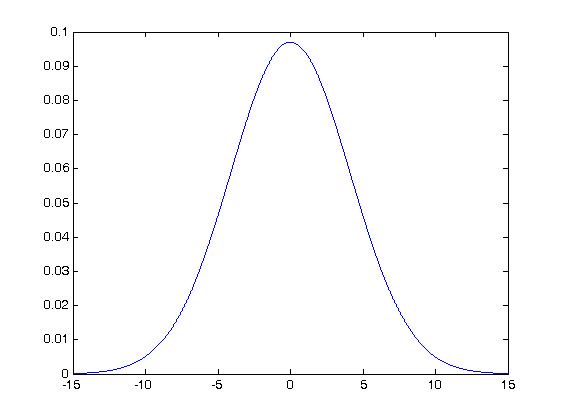
Теперь строю график проекции ф.п.р. для найденной дисперсии и нулевого м.о.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.