Изучение алгоритма и основных свойств дискретного фильтра Калмана

6.  ОПТИМАЛЬНАЯ ФИЛЬТРАЦИЯ СЛУЧАЙНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ

Цель работы: изучение алгоритма и основных свойств дискретного фильтра Калмана.

6.1.Методические указания по подготовке к работе

При построении оптимального рекуррентного алгоритма дискретной задачи фильтрации предполагается, что оценка на текущем шаге  вычисляется с использованием текущего измерения y[k], оценки  и соответствующей ей матрицы ковариаций ошибок P[k – 1] для предыдущего шага. В случае линейной задачи фильтрации для описания модели измерений и динамики изменения вектора состояния x[k] используется система уравнений

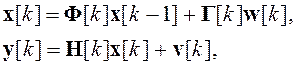
где w[k] – вектор порождающих дискретных белых шумов с матрицей ковариаций Q[k]; v[k] – вектор белых шумов измерений, не коррелированный с вектором w[k], с матрицей ковариаций R[k]; F[k] – матрица перехода из k–1-го состояния в k-е; G[k] – матрица возмущений; H[k] – матрица измерений.

Дискретный фильтр, минимизирующий средние квадраты составляющих вектора ошибок , представляет собой оптимальный фильтр Калмана, описываемый уравнениями

,

,

,

,

,

где  – экстраполированная оценка состояния, S[k] – матрица ковариаций ошибок экстраполяции; K[k] – матричный коэффициент усиления фильтра Калмана.

Начальными условиями для алгоритма калмановской фильтрации является начальная оценка , равная априорному математическому ожиданию вектора состояния, и начальная матрица ковариаций вектора ошибок P[0], равная априорной матрице ковариаций вектора состояния.

6.2.Порядок выполнения лабораторной работы

1.  Открыть m-файл, содержащий программу моделирования случайной последовательности в соответствии с вариантом задания к работе 5.

2.  Сформировать дискретные измерения в виде суммы отсчетов промоделированной случайной последовательности и дискретного белого шума. Среднеквадратическую ошибку измерений принять равной единице.

3.  Сформировать алгоритм обработки измерений в виде дискретного фильтра Калмана.

4.  Построить графики ошибок измерений для каждой компоненты вектора состояния и соответствующих им значений ±3s, вычисленных по ковариационной матрице, рассчитываемой в фильтре.

Пример выполнения задания приведен в Приложении.

6.3.Оформление отчета

Отчет о лабораторных исследованиях должен содержать:

-  исходные данные;

-  модель динамики и модель измерений в форме пространства состояний;

-  алгоритм фильтра Калмана;

-  текст m-файла, с помощью которого получены оценки переменных состояния;

-  графики ошибок оценок и соответствующих им значений ±3s;

-  выводы по работе.

6.4.Контрольные вопросы

1.  Сформулируйте постановку линейной задачи рекуррентного оценивания дискретной случайной последовательности, заданной с помощью формирующего фильтра.

2.  Какие основные блоки содержит алгоритм дискретного фильтра Калмана?

3.  Поясните, почему алгоритм фильтра Калмана является рекуррентным.

4.  Поясните, что такое ошибки прогноза и ошибки фильтрации.

5.  Почему ошибки фильтрации являются марковской последовательностью?

6.  При каких условиях существует установившийся режим в задаче фильтрации?

7.  Что такое фильтр Винера? Поясните его связь с фильтром Калмана.

8.  В чем заключается особенность алгоритмов фильтрации при наличии ненулевой корреляции между порождающими и измерительными шумами?

ПРИЛОЖЕНИЕ

Текст m-файла к примеру выполнения работы

clear; close all;

N = 1000; %число отсчетов случайного процесса

%Параметры случайного процесса

sig = 1.5;

alf = 0.5;

bet = 2;

sigv = 1; %ско измерений

dt = 0.01; %период дискретности

%Формирование непрерывной модели динамики

F = [0 1; -(alf^2 + bet^2) -2*alf];

G = [0; sig*sqrt(2*alf)];

H = [sqrt(alf^2 + bet^2) 1];

%Дискретизация непрерывной модели

Fi = eye(2) + F*dt;

Gam = G*dt;

Q = 1/dt;

%Формирование начального состояния фильтра

P = [sig^2/2/(alf^2 + bet^2) 0; 0 sig^2/2];

x = sqrt(P)*normrnd(0,1,2,1);

xo = [0; 0]; %начальная оценка

%Инициализация массивов

%для записи результатов моделирования

y(N) = 0;

Xo(2,N) = 0;

sko(2,N) = 0;

X(2,N) = 0;

%Формирующий фильтр

w = normrnd(0,1/sqrt(dt),1,N); %порождающий шум

v = normrnd(0,sigv,N,1); %шум измерений

for k = 1:N

    x = Fi*x + Gam*w(k);

    y(k) = H*x + v(k);

    X(:,k) = x;

end;

%обработка измерений

R = sigv^2;

Pe = P;

for k=1:N

    xp = Fi*xo;                  %Прогноз

    S = Fi*Pe*Fi' + Gam*Q*Gam';  %Ковариация прогноза

    K = S*H'*(H*S*H' + R)^-1;    %К.у. фильтра Калмана

    xo = xp + K*(y(k) - H*xp);   %Оценка

    Pe = (eye(2) - K*H)*S;       %Ковариация ошибок

    Xo(:,k) = xo;          

    sko(:,k) = sqrt(diag(Pe));

end;

%Построение графиков ошибок оценивания

t = (0:N-1)*dt;

figure;

plot(t,X(1,:) - Xo(1,:));

hold on;

plot(t,3*sko(1,:),'r--');plot(t,-3*sko(1,:),'r--');

xlabel('t, c');

ylabel('\epsilon_1');

title('Ошибка оценки переменной x_1');

figure;

plot(t,X(2,:) - Xo(2,:));

hold on;

plot(t,3*sko(2,:),'r--');plot(t,-3*sko(2,:),'r--');

xlabel('t, c');

ylabel('\epsilon_2');

title('Ошибка оценки переменной x_2');