СПбГУАП
Кафедра №
Рейтинг за работу ______________
Преподаватель Лопарев А.В.
Отчет
о лабораторной работе по курсу
«Цифровые системы управления и обработки информации»
«Восстановление непрерывного сигнала по его
дискретным отсчетам»
Работу выполнил
Студент группы 1421 Жирков Д.А.
Санкт-Петербург
2008
1.Цель работы.
Восстановление непрерывной функции по ее дискретным отсчетам для трех значений верхней частоты ее спектра:
а) ωв < 0.5*ωд , где ωв - верхняя частота спектра непрерывной функции,
ωд - частота дискретизации спектра.
б) ωв = 0.5*ωд;
в) ωв > 0.5*ωд.
Сделать выводы о возможности восстановления непрерывного сигнала во всех случаях.
Рассмотреть случай увеличения числа периодов сигнала в 50 раз.
2. Порядок выполнения работы.
В программной среде MatLab создаем программу для построения функции по ее дискретным значениям, а также и для построения спектра исходного сигнала и спектра восстановленного сигнала.
а) Рассмотрим случай ωв < 0.5*ωд , а именно:
0.5*ωд=6.28 1/с
ωв=3 1/с
В данном случае, по теореме Котельникова, непрерывная функция должна быть точно восстановлена. Это подтверждается графиком на рисунке 1 «Восстановленная и исходная функции при ωв < 0.5*ωд».
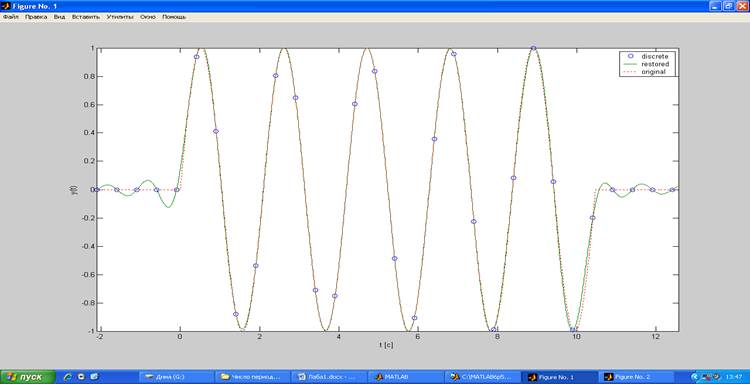
Рис.1. Восстановленная и исходная функции при ωв < 0.5*ωд.
На рисунке 2 представлены графики спектров исходной и восстановленной функции.
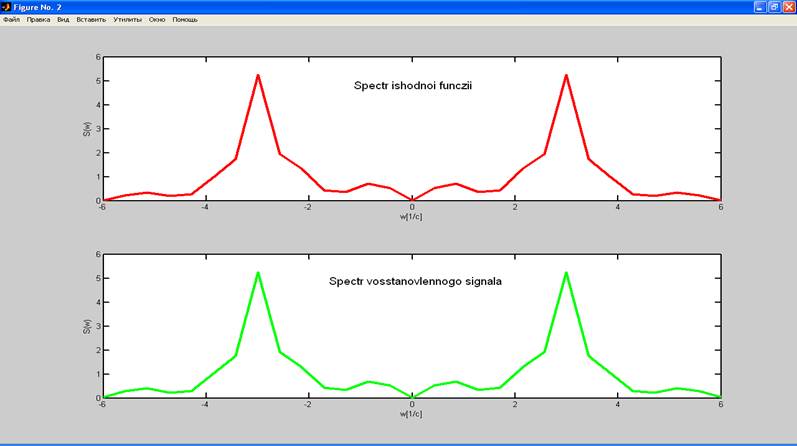
Рис.2. Спектр исходной и восстановленной функции при ωв < 0.5*ωд.
б) Рассмотрим случай ωв = 0.5*ωд, а именно:
ωв=6.28 1/с
В данном случае копии спектра исходного сигнала накладываются друг на друга, что должно привести к появлению ложных частот. Восстановленная и исходная функции приведены на рисунке 3.
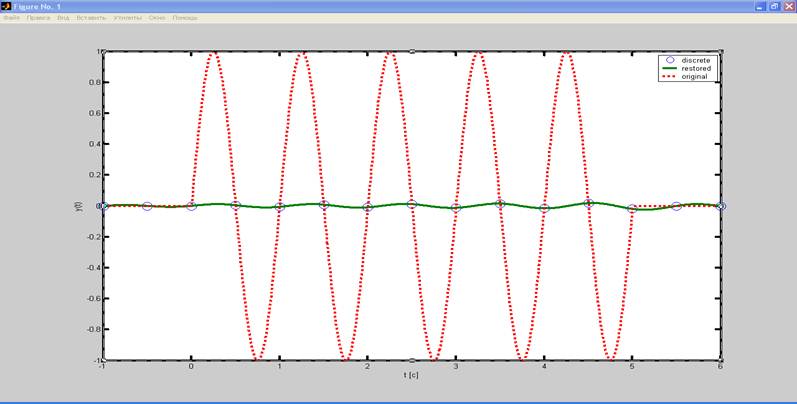
Рис.3. Восстановленная и исходная функция при ωв = 0.5*ωд.
Спектры исходного и восстановленного сигнала представлены на рисунке 4.
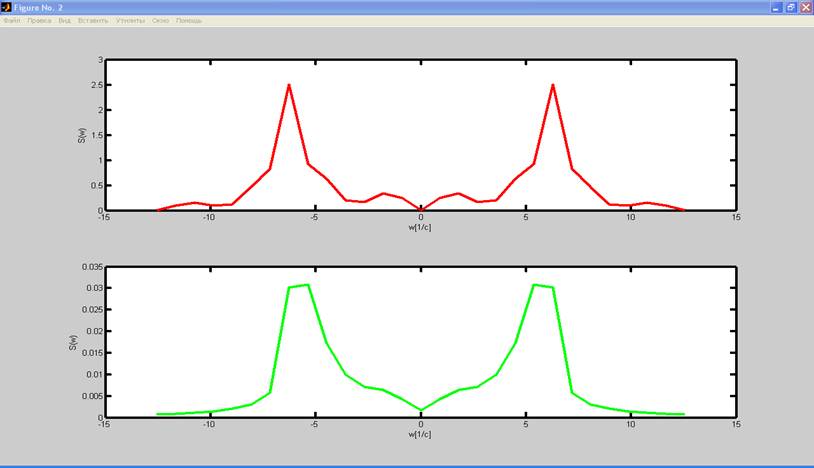
Рис.4. Спектры исходного и восстановленного сигнала при ωв = 0.5*ωд.
в) Рассмотрим случай ωв > 0.5*ωд., а именно:
ωв=12 1/с
В данном случае верхняя частота спектра почти равна частоте дискретизации, что вызовет наложение копий спектра исходного сигнала. Поэтому восстановление исходного непрерывного сигнала по дискретному отсчету с помощью пропускания дискретного сигнала через фильтр с прямоугольной АЧХ приведет к появлению ложных частот.
На рисунке 5 представлен график восстановленной и исходной функции.
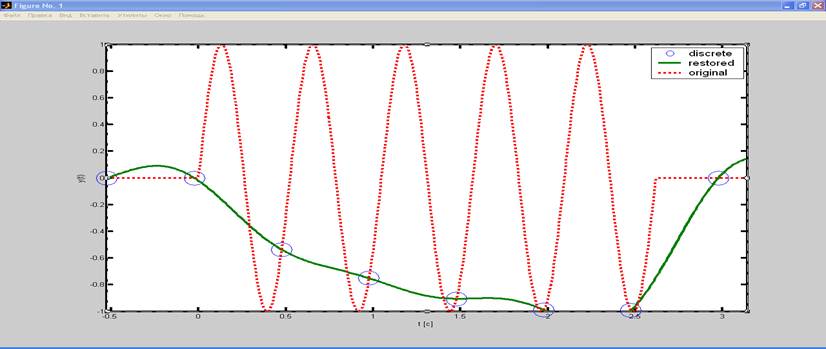
Рис.5. Восстановленная и исходная функции при ωв > 0.5*ωд
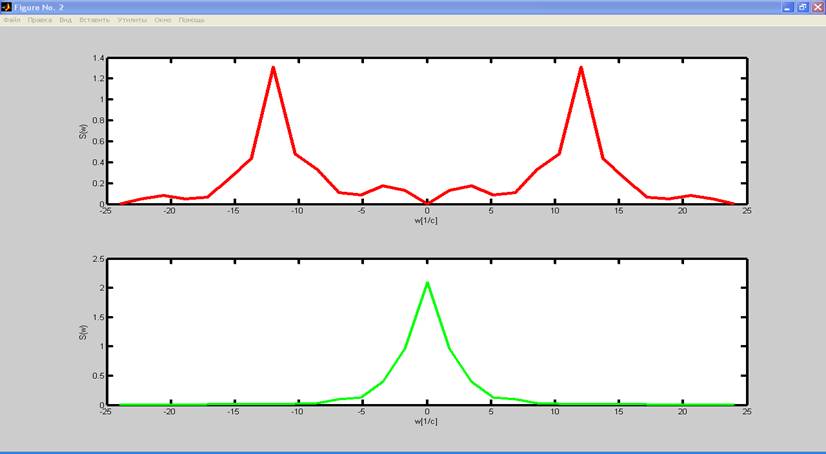
Рис.6. Спектры исходного и восстановленного сигнала при ωв > 0.5*ωд.
Теперь рассмотрим случай, когда число периодов сигнала увеличено в 50 раз до 250. График спектра исходной и восстановленной функции на рис. 7 представлен для случая ωв = 0.5*ωд.
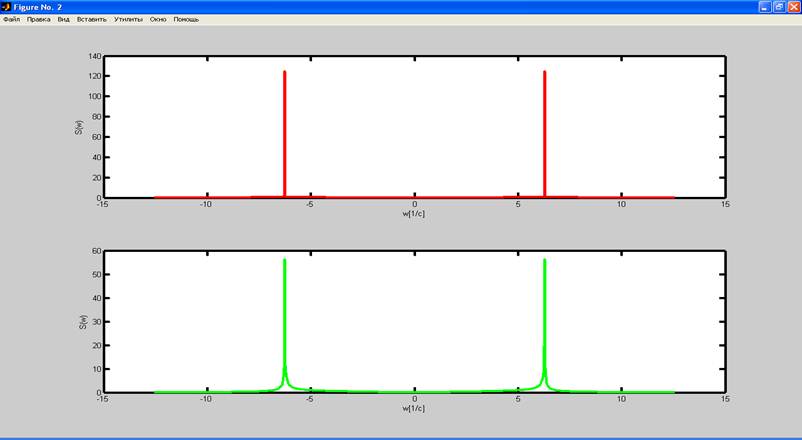
3.Вывод.
В случае, когда ωв < 0.5*ωд , то по теореме Котельникова, непрерывная функция должна быть точно восстановлена. Это подтверждается графиком на рисунке 1.
В случае, когда ωв = 0.5*ωд , копии спектра исходного сигнала накладываются друг на друга, что приводит к появлению ложных частот. См. рисунок 3.
В случае, когда ωв > 0.5*ωд , копии спектра все больше накладываются друг на друга, что вызывает все большее наложение частот до тех пор, пока эта ложная частота не получит максимум в точке ωв = K*ωд, где К-целое число. Поэтому восстановление исходного непрерывного сигнала по дискретному отсчету с помощью пропускания дискретного сигнала через фильтр с прямоугольной АЧХ приведет к появлению ложных частот.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.