1. АНАЛИТИЧЕСКИЙ ОБЗОР
ОСНОВЫ ТЕОРИИ СВЯЗИ ПО ЛИНИЯМ ЭЛЕКТРОПЕРЕДАЧИ
Распространение токов высокой частоты по проводам линий электропередачи описывается с помощью так называемых телеграфных уравнений, дающих возможность определить токи и напряжения в каждом проводе, в любой точке линии по их значениям в начале или конце линии.
Эти уравнения и их решения тем сложнее, чем больше в линии проводов и неоднородностей, к которым относятся несогласованные нагрузки, ответвления, транспозиции и др.
Наиболее простой одноволновой системой является однопроводная линия, в которой обратным проводом является земля. Такая линия характеризуется одной постоянной передачи g = b + ja и одним волновым сопротивлением Zc. Токи и напряжения в любой точке однопроводной линии, нагруженной на согласованную нагрузку Zе = Zc (рис.1-1), определяются выражениями:
Uх = U0е-gх ;
Iх = I0е-gх ; (1-1)
Uх/Iх = U0/I0 = Zc
Вторичные параметры линии g и Zс связаны с первичными параметрами R,L,G и С — сопротивлением, индуктивностью, проводимостью изоляции и емкостью на единицу длины следующими формулами:
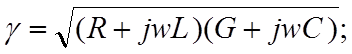 (1-2)
(1-2)
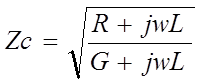 ,
(1-3)
,
(1-3)
w = круговая частота (w = 2pf).
Для высоких частот, когда jwL >> L и jwC >> G, эти формулы можно упростить
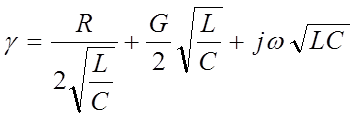 ; (1-4)
; (1-4)
Zc = 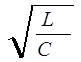 .
(1-5)
.
(1-5)
На линиях электропередачи, благодаря хорошей изоляции проводов, проводимость изоляции G весьма мала и можно пренебречь вторым членом (1-4). Тогда (1-4) можно записать так:
g = 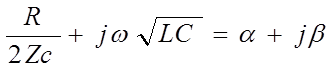 (1-6)
(1-6)
Активная составляющая (1-6) выражает затухание линии на единицу длины (обычно на 1 км), коэффициент при j означает изменение фазового угла на единицу длины:
километрическое затухание
a = R/2Zc; (1-7)
угловой коэффициент
b = w![]() ,
(1-8)
,
(1-8)
так
как b = w![]() ,
где n —
фазовая скорость, то
,
где n —
фазовая скорость, то
n = 1/![]() .
(1-9)
.
(1-9)
Если нагрузка на конце линии Zе ¹ Zс, то появятся отражённые волны и выражения для определения токов и напряжений в различных точках линии примут следующий вид:
Uх = U0×chgх-I0×Zе×shgх;
Iх = I0×сhgх-U0/Zе×shgх; (1-10)
Если в (1-10) вместо Zе поставить Zс, получим (1-1).
Из (1-10) можно получить телеграфные уравнения, связывающие напряжение и ток в начале линии с их значениями на конце:
U0 = Uе × сh g l + Iе ×Zе × s h g l ;
Iх = Uе/Zc × ch g l + Iе × sh g l ; ( 1-11)
Входное сопротивление линии:
Z вх
= ![]() = Zc
= Zc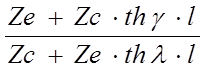 ;
(1-12)
;
(1-12)
Из (1-12) видно, что при Zе = Zс имеем Zвх = Zс.
Ёмкость и индуктивность линии являются величинами практически постоянными, и поэтому в спектре высоких частот волновое сопротивление Zс и скорость n меняются мало.
Километрическое затухание a зависит от сопротивления R, которое
растёт с увеличением частоты. Сопротивление про![]() водов
благодаря поверхностному эффекту увеличивается пропорционально Öf.
водов
благодаря поверхностному эффекту увеличивается пропорционально Öf.![]()
![]()
![]()
![]()
![]()
![]()
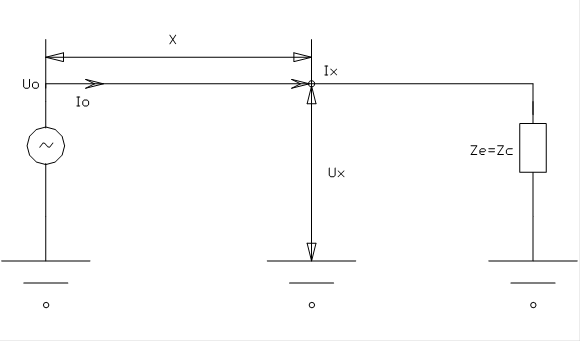 |
Рис. 1-1. Однопроводная линия с согласованной нагрузкой.
Поэтому затухание канала в системе провод — провод двухпроводной линии, достаточно удалённой от земли, также пропорционально Öf.
В системе провод — земля (рис. 1-1) затухание растёт круче, так как сопротивление земли быстро увеличивается с ростом частоты.
Распространение энергии по двухпроводной линии происходит по двум путям (волновым каналам): провод-провод и два провода-земля. В некоторых схемах присоединения используется только один из этих волновых каналов.
На рис. 1-2 показана двухпроводная симметричная линия, характеризующаяся размерами d, S и h (рис. 1-2,а). В схеме на рис. 1-2,б будет иметь место только волна провод — провод (междуфазная); в схеме на рис. 1-2,в волна два провода — земля (нулевой последовательности); в схеме на рис. 1-2,г — обе волны, независимо от того, будут ли концы второго провода отключены, заземлены или он будет натружен на сопротивления с одного или обоих концов. Точный расчёт даже такой простейшей двухволновой системы достаточно сложен. Необходимо прежде всего рассчитать параметры (затухания, скорости распространения и волновые сопротивления) обоих волновых каналов. Затем следует разложить токи и напряжения на передающем конце на составляющие этих каналов и суммировать их на приемном конце с учетом концевых условий.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.