Исследование возможностей расширения частотного диапазона для ВЧ связи по ЛЭП до 1000 кГц (Аналитический обзор дипломного проекта), страница 5

Линия, бесконечно простирающаяся в одну сторону от конечной точки  (« полубесконечная линия »), описывается выражением:

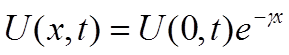                                                                 (1-21)

Для n -проводной линии без потерь имеет место 2n уравнений, связывающих токи и напряжения в любой точке z линии:

  

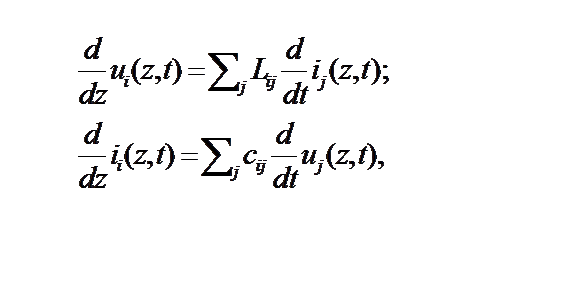
(1- 22)                

(1- 23)

где и  — собственные  и  взаимные   индуктивности   проводов рассматриваемой д-проводной системы.

Уравнения (1-23) и (1-24) могут быть записаны в матричной форме:

½u (z, t)½- столбцовая матрица напряжений u(z, t);

½i (z, t) ½- столбцовая матрица токов i(z, t);                                       

½L ½- квадратная матрица индуктивностей L;

½С½- квадратная матрица ёмкостей С;

Применение указанных матричных обозначений упрощает   запись 2n уравнений типа (1-22) и (1-23)

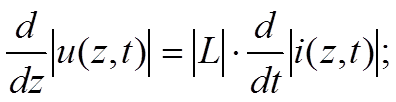
(1-24)

Допуская, что на высоких частотах токи проходят по поверхности проводов земли, устанавливаем формальную идентичность матриц |L| и |С|, различающихся лишь по коэффициентам.

Если   ½N½ — нормализованная матрица преобразования, общая |L| и  |С|, то для случая трехфазной  линии она записывается в виде:

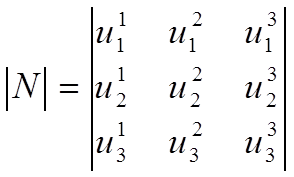                                                             (1-25)

u—нормализованный коэффициент волнового канала j напроводе.

Коэффициенты uсвязаны уравнением, определяющим условие независимости или « ортонормировки » волновых  каналов:

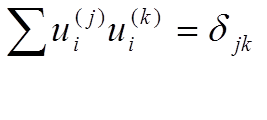
          при  j¹k

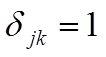            при j=k

С учётом оговоренных выше условий получаем:

                                            (1-26)                                  

                                                            (1-27)

                                                                                 (1-28)

                                                                                 (1-29)

где индекс m означает волновую составляющую.

Отсюда уравнения (1-24) запишутся в виде:

                                                    (1-30)

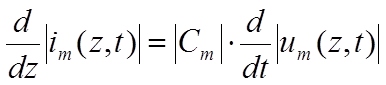                                                  (1-31)

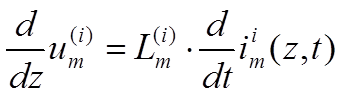                                                              (1-32)

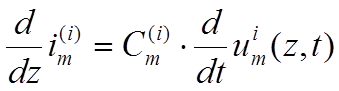                                                               (1-33)

Величины u и i элементов матриц    и   определяются линейной комбинацией напряжений и токов на проводах, как это иллюстрируется раскрытием уравнений (1-26), (1-27) для случая трёхфазной трёхпроводной ВЛ                                                                                                       

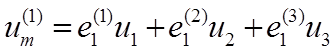                                                         (1-34)

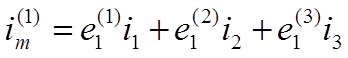                                                      (1-35)

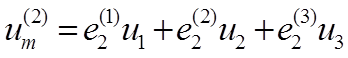                                                      (1-36)

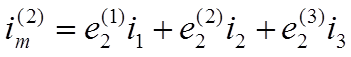                                                      (1-37)

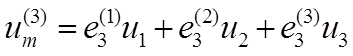                                                      (1-38)

                                                       (1-39)

В уравнениях (1-34) — (1-39) каждая пара напряжение — ток также удовлетворяет уравнениям (1-32) и (1-33). Такие пары уравнений являются аналогами распространения волны напряжения u_м и волны тока i_м вдоль единичного провода над землей. В частности, uи i связаны уравнением      ,где Z — полное волновое сопротивление.

Рассмотренные комбинации уравнений соответствуют волновым каналам распространения.

ВЛ, свободная от отражений. В ряде случаев фазы, неиспользуемые для ВЧ связи, могут быть либо разомкнуты (если они обработаны ВЧ заградителями), либо практически заземлены (через емкость шин подстанции) для высоких частот. Если неиспользуемая для связи фаза линии разомкнута (I=0), уравнения вида:

АI1+ ВI2 + CI3 = U1;

ВI1 + DI2 + ВI3 = U2;                                                                       (1- 40)

CI1 + ВI2 + АI3 = U3;

приводятся к двум или к одному уравнению. Например, если передатчик подключен к средней фазе и подает на нее напряжение Ui, имеем:

   Ui = U2; I1 = I3 = 0; I2 = U2/D;   Pi = U2/D.                               (1- 41)