Промышленность \ Производственные технологические процессы

Определение внутренних напряжений и шероховатости обработанных поверхностей при черновом точении

Страницы работы

7 страниц (Word-файл)

Посмотреть все страницы

Скачать файл

Содержание работы

Лабораторная работа №1

Определение внутренних напряжений и шероховатости обработанных поверхностей

при черновом точении.

Обрабатываем кольца на заданных режимах (таблица 1).

Определяем шероховатость обработанных поверхностей колец с использованием образцов шероховатости и заносим их значения в таблицу 1

Замеряем диаметры колец , после обработки образцов (в 2-х сечениях),затем разрезаем кольца и замеряем их диаметр .Внутренний диаметр кольца d=36.75

Таблица 1

Экспериментальные данные.

Вид обработки	Режим обработки		Шероховатость, Ra	Диаметр			Диаметр
Вид обработки	Режим обработки		Шероховатость, Ra	1-й замер	2-й замер	Среднее	1-й замер	2-й замер	Среднее
Черновое а) точение б)	n=250 об/мин t=3 мм	=0.3	12,5	41,34	41,25	41,295	41,4	41,4	41,4
		=0.5	20	41,74	41,64	41,69	42,3	41,99	42,145
		=0.7	32	42,01	41,99	42	42,22	42,33	42,275
	n=250 об/мин S=0.5 мм/об	=3	20	41,86	41,7	41,78	42,08	42,18	42,13
		=2	15	43	43	43	43,01	43,11	43,06
		=1	10	43,12	43,12	43,12	43,16	43,16	43,16

Определение значения напряжений и при принятых методах и режимах обработки и результаты заносим в таблицу 2.

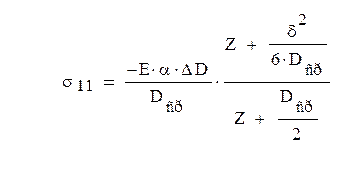
Напряжения, снятые при разрезке колец. где E-модуль упругости, который для стали E=

-коэффициент

-коэффициент Пуассона

Z-расстояние между средней линией кольца после обработки и серединой рассматриваемого (снятого слоя) металла:

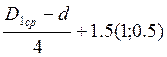
-толщина стенки кольца после обработки

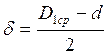
диаметр срединной окружности обработанного кольца до разрезки

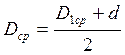
- измеренное изменение наружного диаметра кольца после разрезки

Величина полных тангенциальных напряжений

где k=30-коэффициент

Вид обработки	Режим обработки				Z	d	,	,
Точение черновое а)	n=250 об/мин t=3 мм	S1=0.3	-0,105	39,023	2,636	2,273	7,099	212,963
		S2=0.5	-0,455	39,220	2,735	2,470	31,507	945,207
		S3=0.7	-0,275	39,375	2,813	2,625	19,388	581,637
б)	n=250 об/мин S=0.5 мм/об	t1=3	-0,350	39,265	2,758	2,515	24,365	730,939
		t2=2	-0,060	39,875	2,563	3,125	3,827	114,801
		t3=1	-0,040	39,935	2,093	3,185	2,131	63,917

Определение параметров эмпирической зависимости для одного основного фактора.

Вид зависимости:

Используется система из двух уравнений с двумя неизвестными ():

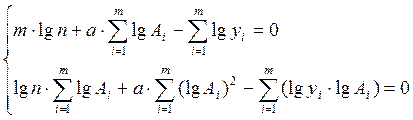
Вводится замена.

; ; ;

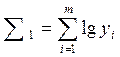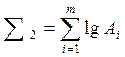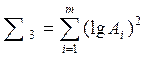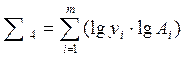
Тогда уравнение примет вид:

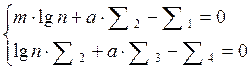
Из системы определяются lgn и a.

Определение параметров эмпирической зависимости Ra=f(S)

Таблица 1

Определение числовых значений системы уравнений.

i	Rai	Si	lgRai	lgSi	lgSi^2	lgSi*lgRai
1	12,5	0,3	1,097	-0,523	0,273	-0,574
2	20	0,5	1,301	-0,301	0,091	-0,392
3	32	0,7	1,505	-0,155	0,024	-0,233
Суммы			S2	S5	S3	S6
			3,903	-0,979	0,388	-1,198

Продолжение таблицы 1

i	a*lgSi	Si^a	Rabi=n*Si^a	Rabi-Ra	(Rabi-Ra)/Rai*100%
1	-0,572	0,268	12,188	-0,312	2,493%
2	-0,329	0,468	21,313	1,313	6,564%
3	-0,169	0,677	30,797	-1,203	3,761%

Т.о. эмпирическая зависимость имеет вид Ra=45,495*Si^1,094

Определение параметров эмпирической зависимости Ra=f(t)

Таблица 2

1 2 3

Информация о работе

ВУЗ:

Гомельский государственный технический университет им. П.О. Сухого (ГГТУ им. Сухого)

Предмет:

Производственные технологические процессы

Тип:

Отчеты по лабораторным работам

Категория:

Промышленность (Технические предметы)

Размер файла:

251 Kb

Скачали:

Скачать файл

Определение внутренних напряжений и шероховатости обработанных поверхностей при черновом точении

Страницы работы

Содержание работы

Похожие материалы

Информация о работе