Выборка – конечный набор значений случайной величины, полученый в результате наблюдений. Число элементов выборки называют её объёмом и обычно обозначают N. Выборки подразделяются на повторные и безповторные. Повторной называют выборку, при которой отобранный объект возвращается в генеральную совокупность, а безповторной – выборку, при которой отобранный объект в генеральную совокупность не возвращается.
Смысл статистических методов заключается в том, чтобы по выборке ограниченного объема N, т.е. лишь по некоторой части генеральной совокупности, высказать обоснованное суждение о её свойствах в целом. Подобное суждение может быть получено путем построения эмпирических (выборочных) аналогов вероятностных характеристик исследуемой величины, иначе говоря, путём оценивания параметров (характеристик) генеральной совокупности с помощью некоторых подходящих функций от результатов наблюдений – оценок.
Если перефразировать последнее предложение получим определение оценки.
Оценка – эмпирический аналог вероятностной характеристики генеральной совокупности, рассчитываемый как функция от результатов наблюдений.
Таким образом, теперь мы можем ответить на вопрос, в чём же
разница между mх и 
и sx и Sx: mх и sx – теоретические, вероятностные характеристики совокупности, а и Sx – их оценки (или иначе выборочные, эмпирические
аналоги).
Возникает следующий вопрос. На каком основании мы можем их
заменять (mх на и sx на Sx)?
Теоретическое обоснование выборочного метода(или, иначе, применимость оценок) дают две теоремы: Чебышева и Ляпунова.
Согласно теореме Чебышева при достаточно большом объеме выборки разность между выборочной характеристикой (оценкой) и генеральной характеристикой совокупности будет сколь угодно малой с вероятностью близкой к единице.
А при определенном объеме выборки (n) работает теорема Ляпунова, по которой можно рассчитать эту разницу Δ (между параметром генеральной совокупности и ее оценкой), которая определяет ошибку выборки.
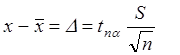
где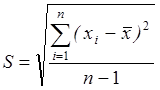 
- есть
среднеквадратическое отклонение выборки,
n - объем выборки(число измерений) ;
-
выборочная средняя, т.е. среднее арифметическое значение;
tnα - коэффициент Стьюдента, который меняется в зависимости от вероятности α и величины k=n-1.
Из формулы следует , что с увеличением объема выборки ошибка выборки Δ уменьшается.
С точки зрения практики к свойствам оценок предъявляются требования:
1.Состоятельность. Оценка
называется состоятельной, если при неограниченном увеличении объема выборки (n→∞), значение оценки стремится к своему теоретическому
значению ( → mx).
2.Несмещенность. Она означает отсутствие систематической погрешности при оценивании параметра.
3.Эффективность. Она предполагает минимальную дисперсию; следовательно, эффективная оценка имеет минимальную случайную ошибку.
Оценки могут быть: (1) точечными и (2) интервальными.
1. Точечная оценка задается одним числом, получаемым путем подстановки выборочных значений X1 , X2 , … , Xn в формулу для оценки искомого параметра.
Например, (как уже отмечалось ранее) математическое ожидание mx и дисперсия sx оцениваются по формулам:
;
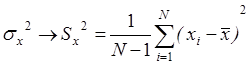
Использование в знаменателе формулы дисперсии величины ν = N-1 (ν- число степеней свободы) вместо очевидного на первый взгляд значения N продиктовано необходимостью достижения свойства несмещенности. Поправка λ = N/(N-1) называется мультипликативной поправкой Бесселя.
Однако точечные оценки не дают информации о степени близости оценки к соответствующему теоретическому параметру. Поэтому более информативной является интервальная оценка, дающая представление о степени точности и надежности оценки для параметра.
2. Интервальная или доверительная оценка – это интервал, который с определённой вероятностью γ охватывает оцениваемое значение Х.
Таким образом интервальная (доверительная) оценка характеризуется двумя величинами:
(1). Шириной доверительного интервала Δ, которая является мерой точности оцениваемого параметра (чем меньше Δ для данного γ, тем точнее оценка).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.