Циклический алгоритм исследования. Типы измерений и характер ошибок в них, страница 5

2.         Графический:

2.1.      в виде гистограммы.

При построении гистограммы в прямоугольных                        n

координатах по оси абсцисс – откладывают границы интервалов, а по оси ординат – соответствующие абсолютные или относительные частоты. На гистограмме

каждая группа изображается прямоугольником, ширина которого пропорциональна ширине                                                                  x группы, а высота – частоте. Площадь отдельных прямоугольников прямопропорциональна групповой частоте, а площадь всех прямоугольников – общему числу наблюдений.

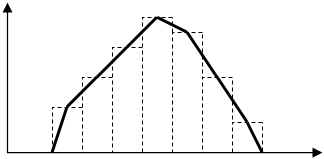
2.2.     в виде полигона.

n                                                                                 Полигон получается, если соединить отрезками прямых середины верхних сторон прямоугольников.

 

x 

3.         Аналитически (в виде формулы)

Cуществует два аналитических способа выражения закона распределения случайных величин, а именно, две функции распределения вероятностей:  интегральная и дифференциальная.

(I) Интегральная функция распределения F(x) случайных величин Х показывает вероятность того, что случайная величина не превышает некоторого заданного или текущего значения х, т.е.

F(x) = P{Х≤х}

Через P «большое» обозначают оператор вероятности, через р «малое» – конкретную величину вероятности.

Следовательно, вероятность того, что значение случайной величины Х заключено между x₁ и x₂ равна разности значений функций распределения, вычисленных в этих двух точках.

P{x₁<Х≤x₂}=F(x₂)-F(x₁)

Основные свойства интегральной функции распределения:

(1)  lim F(X) = F(- ∞) = 0

x→ - ∞

(2)  lim F(X) = F(+ ∞) = 1

x→ + ∞

(3)       F(X) ≥ 0 для всех Х

(II) Дифференциальная функция распределения вероятностей, которую иначе еще называют функцией плотности распределения вероятностей и обозначают f(x )

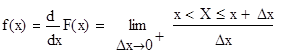
C помощью дифференциальной функции легко определяется вероятность нахождения случайной величины  в любой области из множества ее возможных значений.       

Основные свойства дифференциальной функции распределения:

(1)       lim f(X) = 0

x→ ∞

(2)      

(3)       f(X) ≥ 0 для всех Х

Как интегральная, так и дифференциальная функции распределения являются исчерпывающими вероятностными характеристиками случайной величины. Однако основные свойства случайных величин могут быть описаны более просто с помощью отдельных числовых параметров. Наиболее важными из них являются математическое ожидание М(х) (теоретическая средняя) и дисперсия D(x):

1. Центр распределения или, иначе, центр группирования, вокруг которого сосредоточено все распределение, характеризуется математическим ожиданием М(х) случайной величины х :

Математическое ожидание часто ещё называют генеральным средним значением или теоретическим средним.

2. Степень рассеяния случайной величины х относительно её математического ожидания М(х) характеризуется с помощью генеральной дисперсии  s_x².

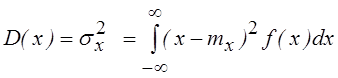
Квадратный корень из дисперсии s_x² называется средним квадратическим отклонением s_x.

Физический смысл средне квадратического отклонения: он показывает насколько тесно группируются  значения Х вокруг среднего (или математического ожидания).

Дисперсию еще иначе можно записать как центральный момент второго порядка.

D(x)=m₂=M([x-M(x)]²)

Важными характеристиками распределения так же являются центральные моменты третьего и четвертого порядка. Это асиметрия и эксцесс соответственно.

3. Асиметрия  случайной величины Х — центральный момент третьего порядка.

m₃₌M([x-M(x)]³)

Чаще используют нормированный коэффициент асиметрии a₃:

a₃=m₃/s³

Асиметрия характеризует степень симметричности графика плотности распределения случайной величины относительно среднего значения М(х).

m₃>0                                                               m₃<0                                       m₃=0

f(x)                                         f(x)                                         f(x)

 

m_{x                                            X}                                                                        m_{x    X}                                            m_{x                      X}