Циклический алгоритм исследования. Типы измерений и характер ошибок в них, страница 10

II. Расчет оценок основных числовых параметров распределения.

Окончательно результат измерения или истинное значение измеряемой величины В представляется в виде:

, вероятность Р = g.

где В – символ измеряемой величины,  - ее точечная оценка (результат измерения, вычисленный по формуле), D = D_S - суммарная погрешность или ширина доверительного интервала.

2.1 Расчет точечной оценки.

2.2 Расчет интервальной оценки (ширины доверительного интервала)

Расчет D_S для случаев прямых и косвенных измерений рассмотрен ранее.

Из всей приведенной выше схемы нерассмотренным остался только п.1.4.

п.1.4. Проверка гипотезы

Проверка гипотезы осуществляется с помощью критериев согласия. В общем случае критерий статистической гипотезы – это правило, позволяющее принять или отвергнуть данную гипотезу на основании выборки. А критерий согласия – это один из критериев гипотезы о том, что генеральная совокупность величины x подчинена закону распределения f(x), выбранному исследователем. Подобные критерии основаны на выборе определенной меры расхождения между теоретическим (выбранным исследователем) и эмпирическим распределениями. Если такая мера расхождения (т.е. критерий) для рассматриваемого случая превосходит установленный предел, то гипотеза отвергается, и обратно. Интересно отметить, что и в том и в другом случае (имеется в виду и в случае принятия и в случае отвержения гипотезы) может быть совершена ошибка. Эти ошибки являются характеристики критерия. Существует две характеристики:

(1)  Уровень значимости критерия a – или ошибка I-го рода, когда отвергается истинная f(x);

(2) Мощность критерия 1-b, где b - ошибка II-го рода, когда принимается ложная f(x).

Эти случаи можно представить в виде таблицы.

Гипотеза Решение	Верна	Неверна
Принять	Решение правильно P = 1 - a	Ошибка II-го рода P = b
Отвергнуть	Ошибка I-го рода P = a	Правильное решение P = 1 - b

Величины вероятностей ошибок a и b и объем выборки связаны функциональным соотношением (для каждого из критериев оно свое). При заданном объеме выборки N и выбранном критерии уменьшить одновременно a и b невозможно: если уменьшить a, то b будет возрастать, и наоборот. Например, если принять a = 0 – то будут приниматься все выбранные теоретические f(x), в том числе и неверные. Следовательно возрастет вероятность ошибок II-рода. Единственный способ уменьшить одновременно вероятности ошибок I-го и II-го рода состоит в увеличении объема выборки. a обычно выбирают в пределах от 0,1 до 0,01. Часто уровень значимости a выражается в процентах и показывает сколько раз в ста испытаниях мы рискуем ошибиться. Например, если a = 0,05 – значит мы рискуем ошибиться 5 раз.

Какие бывают критерии согласия?

I.  Наиболее употребляемым на практике является универсальный критерий Пирсона c². Он основан на определении величины c² по формуле:

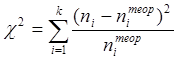
а, затем, сравнении c² с c²_кр. При этом критическое значение критерия согласия (c²_кр) выбирается из таблицы по уровню значимости a. Если c² > c²_кр – то гипотеза отвергается (при этом мы можем совершить ошибку I-го рода с вероятностью a). Если c² < c²_кр – гипотеза принимается (с вероятность b мы можем при этом совершить ошибку тоже).

Как рассчитать c²?

Пусть имеем N значений случайной величины x.

(1)  Строим гистограмму опытного распределения:

1.1   Строим вариационный ряд, где x₀ – min, x_k – max значение x.

1.2   Разбиваем ряд на интервалы, группируем.

1.3   Вычисляем n_i – эмпирические частоты для каждой группы (участка, интервала) от x_i-1 до x_i при этом .

(2)  Рассчитываем теоретические частоты n_i^теор, соответствующие закону распределения f(x). Например, для нормального закона Гаусса n_i^теор будет рассчитываться по формуле:

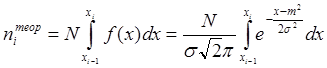
II.  Критерий Колмогорова и Смирнова.

Применяется, если число наблюдений невелико и вид теоретического распределения полностью известен из физического смысла.

Критерий (мера расхождения) рассчитывается по формуле:

, где n – объем выборки.

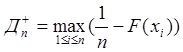
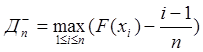
III.       Критерий Крамера-Мизеса-Смирнова w_n².

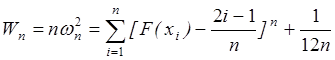
Недостаток –громоздcкость расчетов.