Структурные (алгоритмические) схемы автоматических систем. Передаточные функции типовых соединений звеньев. Правила преобразования структурных схем

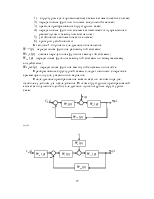
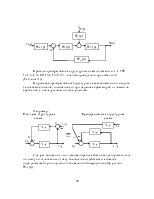
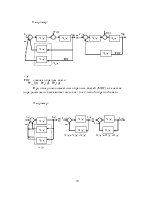
Если требуется исследовать влияние только возмущающего воздействия, то

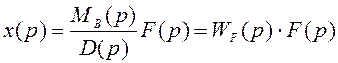                                                      (2.13)

            Рассмотрим определение временных характеристик с помощью формул Хевисайда (путем разложения на простые дроби) для любого из выражений (2.11) - (2.13).

            В качестве примера возьмем выражение (2.12) и рассмотрим следующие случаи:

            1) , , тогда .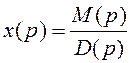

            Если все корни действительны, то оригинал импульсной переходной функции в форме Хевисайда

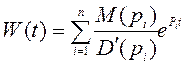                                                                                (2.14)

где 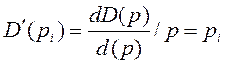                                                                   (2.15)

            Если среди n корней есть S пар комплексно-сопряженных корней, а остальные r корней действительные, то

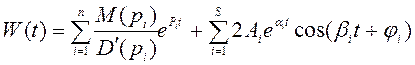             ,                            (2.16)

где      ,   ,        

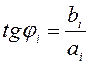
Коэффициенты   и  определяются из выражения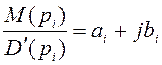         

            Если в характеристическом уравнении кратных корней, тогда

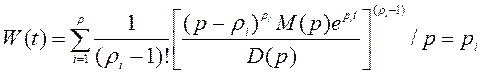                              (2.17)

 где-кратность i –го корня.

            2), , 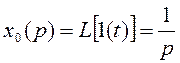тогда 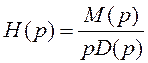, т.е  в выражении

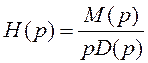  имеется нулевой корень.

            При наличии одного нулевого корня, r – действительных  корней, S – пар комплексно-сопряженных и - кратных корней.

     

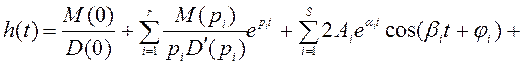
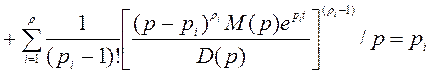                                       (2.18)

            Пример. Определить переходную функцию системы автоматического регулирования, описываемую уравнением вида

            ,

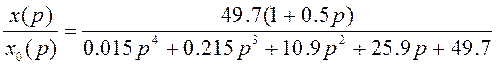откуда

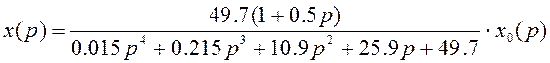  .               (2.19)

            При         ,

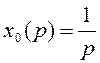тогда

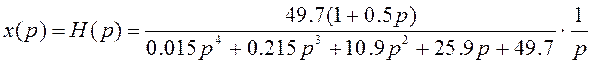           (2.20)

            Решение. Из полинома знаменателя выражения (2.19) определяем корни по методу деления многочленов.

            Характеристическое уравнение системы (полином знаменателя) имеет вид

     ,

или

   .                              (2.21)

            Первое приближение:

               

 или

                                                                              (2.22)

Делим (2.21) на выражение (2.22)   

                

         

                           

                          

                                    

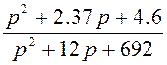
            Второе приближение:

              

или

                                                                                (2.23)

Делим (2.21) на выражение (2.23)

              

             

                            

                       

                                        

                                     

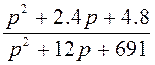
                                            0     -     10p   +      10

            Дальнейшие вычисления проводить нет смысла.

             Таким образом, характеристическое уравнение (2.21) разлагается на два квадратных:

                     и             ,

 или

                                и              .

            Из последних выражений находим корни

               ;

                .

            Итак, выражение (2.20) содержит один нулевой корень и две пары комплексно-сопряженных корней.

            Для нахождения оригинала функции Н(р) воспользуемся выражением (2.18).

            При наличии одного нулевого корня и двух пар комплексно-сопряженных корней выражение (2.18) имеет вид

             

            

          

           

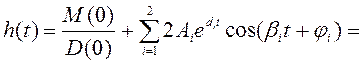
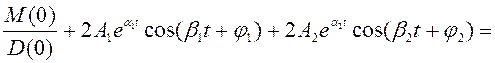
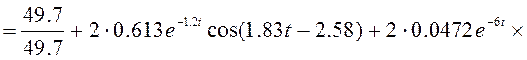
                                                                 (2.24)

 где и - действительная и мнимая части комплексных корней                                                                          .

            Параметры и  определяют при наличии нулевого корня из следующих выражений:

 

при p = pк

            ,

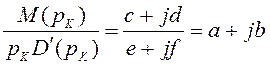при р =                                                                                            (2.25)

         

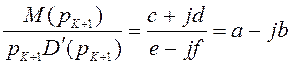
            Выражение (2.25) можно записать в несколько ином виде

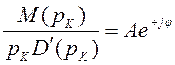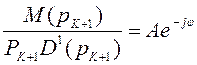            ;   ,                               (2.26)

где  ,   в  .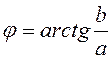

            Для нашего примера

    ,

   .

Вычислим  ;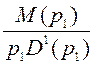

 ;

 ;

                   

 Тогда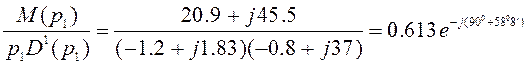

 Откуда ;  или  радиан

            Соответственно

 

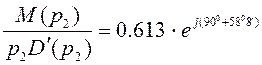
Вычислим  ;     ;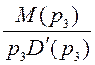

 ;

                    .

Тогда .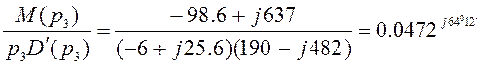

Из последнего выражения имеем  и  радиан

Соответственно

           

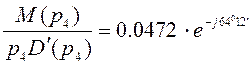
            Если в выражении(2.20) отсутствует нулевой корень, что будет иметь место при определении импульсной переходной функции W(t), то для нахождения А и  используют выражения:

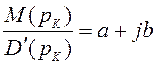     и 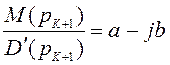                                                         (2.27)

            В таблице 1 представлены передаточные функции как минимально-фазовых, так и неминимально-фазовых динамических звеньев.

            Чтобы избежать возможных ошибок при расчете и построении частотных характеристик, особенно амплитудно-фазовых и фазовых, обратитесь к приложению А (таблицы А3 и А4), в которых приведены графики амплитудно-фазовых, амплитудно и фазо-частотных характеристик типовых звеньев (таблица А3) и логарифмических амплитудно и фазо-частотных характеристик (таблица А4).

            Минимально-фазовыми называются динамические звенья, у которых все корни знаменателя (полюса) и числителя (нули) передаточной функции звена располагаются в левой полуплоскости корней. Минимально-фазовым динамическим звеньям присущи меньшие по абсолютной величине фазовые сдвиги по сравнению со звеньями, имеющими ту же амплитудно-частотную характеристику, но для  которых это условие не выполняется.

            В качестве примера рассмотрим три звена с передаточными функциями:

  ; ; ,                                (2.28)

которые характеризуются тем, что их амплитудно-частотные характеристики совпадают

                                                                                  (2.29)

Запишем выражение для фазо-частотных характеристик этих звеньев:

 ;

 ;

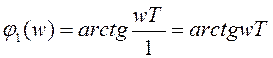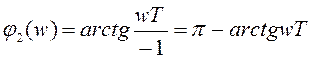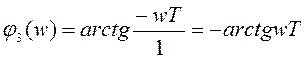                                                            (2.30)