Структурные (алгоритмические) схемы автоматических систем. Передаточные функции типовых соединений звеньев. Правила преобразования структурных схем, страница 2

            Для второго звена в фазо-частотной характеристике  появился дополнительный фазовый сдвиг на  против часовой стрелки, вызванный тем, что амплитудно-фазовая характеристика  при w = 0 равна

            ,                                                                                (2.31)

т.е. АФХ при w = 0 начинается не на положительной вещественной полуоси, являющейся началом отсчета угла в положительном или отрицательном направлении, комплексной плоскости, используемой для построения АФХ, а на отрицательной полуоси.

            Из выражений (2.30) следует, что звено с  имеет большую по абсолютной величине фазу по сравнению со звеном с , поэтому оно является неминимально-фазовым. При одинаковых абсолютных значениях фазы (звенья с  и ) минимально-фазовым является звено с положительной фазой, поэтому звено с  также является неминимально-фазвым .

            Неминимально-фазовые звенья могут быть одновременно и неустойчивыми, например, звено с передаточной функцией

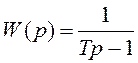             ,                                                                           (2.32)

у которого

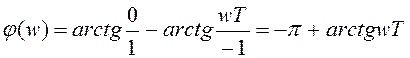                                           (2.33)

является и неминимально-фазовым и неустойчивым.

У звена (2.32) появился дополнительный фазовый сдвиг на  (по часовой стрелке).

            Полную информацию о дополнительных положительных или отрицательных сдвигах в минимально-фазовых и неминимально-фазовых динамических звеньях (системах) дает вид амплитудно-фазовой характеристики (см. таблицу А3), которую желательно рассчитать и построить первой, а затем все остальные.

            При расчете фазовых характеристик динамических звеньев с сомножителями второго порядка следует помнить о следующем.           

            Для колебательного звена с передаточной функцией                                                                                                         

                                  

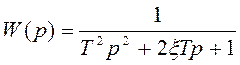
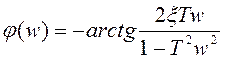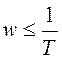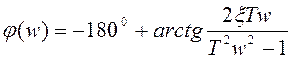                    при ,

       при .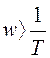

            Для форсирующего звена второго порядка с передаточной функцией

                                 

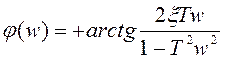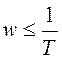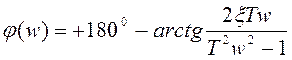                    при ,

       при .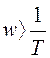

            Для консервативного звена с передаточной функцией                                 

                                      

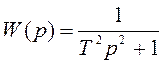
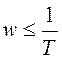
                                               при

                                       при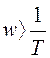

            При построении логарифмических частотных характеристик необходимо иметь в виду то обстоятельство, что для минимально-фазовых систем предельное значение фазовой характеристик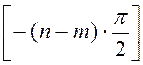и  при  должно соответствовать предельному наклону амплитудной характеристики . Здесь и в дальнейшем под n и  m подразумеваются порядки полиномов знаменателя и числителя передаточной функции разомкнутой системы.

            Для неминимально-фазовых систем это условие не выполняется. Наличие в системе хотя бы одного неминимально-фазового звена свидетельствует о том, что САУ является неминимально-фазовой.

            Все реальные системы  автоматизированного электропривода являются минимально-фазовыми.

 2.2 Методические указания к выполнению домашнего             задания 2.

При выполнении второго домашнего задания изучаются и закрепляются следующие вопросы курса:

1)  структурные (алгоритмические) схемы автоматических систем;

2)  передаточные функции типовых соединений звеньев;

3)  правила преобразования структурных схем;

4)  передаточные функции систем автоматического управления в разомкнутом и замкнутом состояниях;

5)  устойчивость автоматических систем;

6)  критерии устойчивости;

            В таблице 1.2 приняты следующие обозначения:

- передаточная функция разомкнутой системы;

- главная передаточная функция замкнутой системы;

- передаточная функция замкнутой системы по возмущающему воздействию;

- передаточная функция замкнутой системы по ошибке.

            Преобразование структурной схемы следует начинать с переноса сумматора или узла, указанного в варианте.             

            Последующие преобразования можно вести в любом порядке, наиболее удобном для исследования. Итогом структурных преобразований является получение одной из следующих одноконтурных структурных схем:

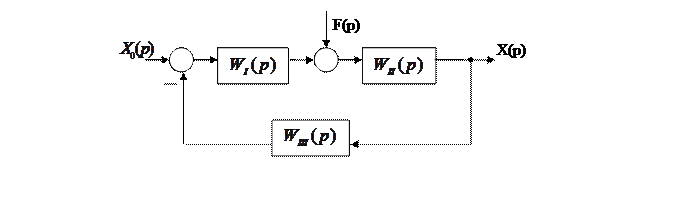
или

F(p)

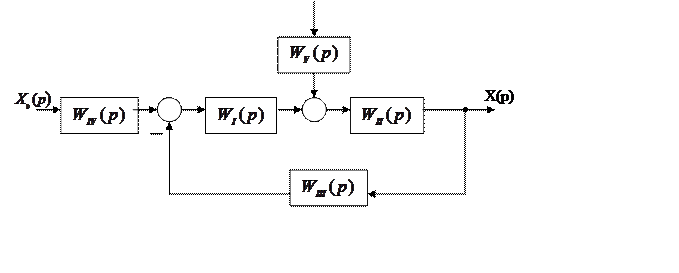
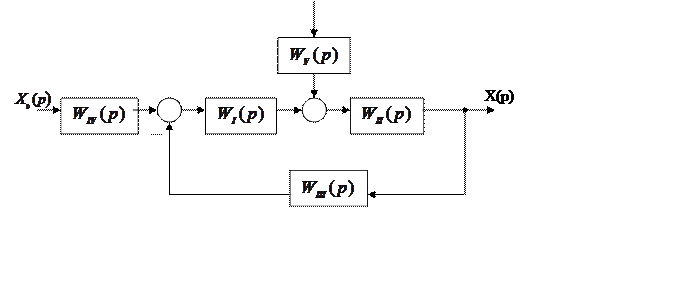
            Правила преобразования структурных схем изложены в /4,С.109-141; 5,С.45-60; 15,С.129-143 /, а также приведены в приложении А (Таблица А5).

            В процессе преобразования структурных схем внимательно следите за знаками сигналов, в особенности при переносе сумматоров и элементов сравнения  с последующим их объединением.

              Например:

Исходная структурная                                Преобразованная структурная                  

             схема                                                                           схема

             

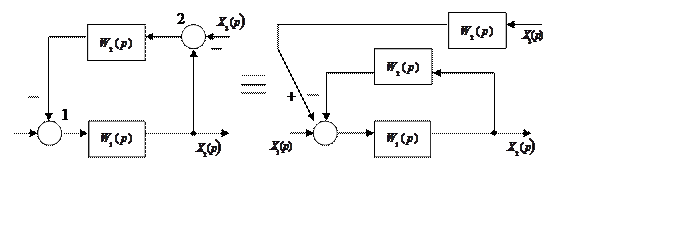
            Следует запомнить, что главная обратная связь всегда отрицательна по знаку по отношению к знаку внешнего воздействия и является определяющей при получении эквивалентной передаточной функции .

           Например:

	F(p)
			F(p)

 

Х(р)

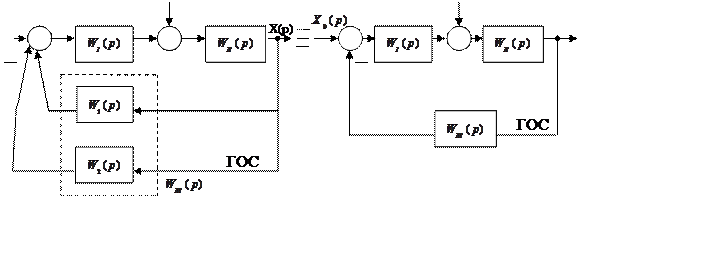
 где

 ГОС- главная обратная связь;

     

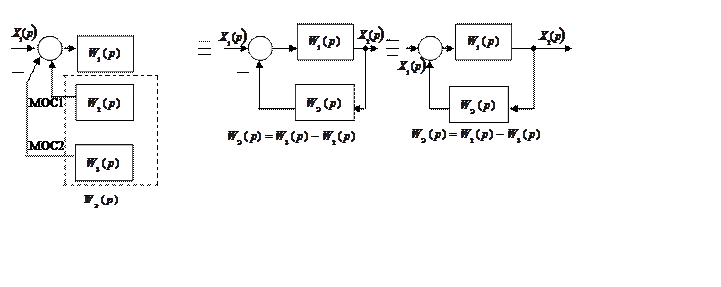
            При объединении местных обратных связей (МОС) в качестве определяющего знака может быть взят знак любой обратной связи.

            Например: