Как уже отмечалось выше, важным параметром метода является требуемая дискретность сетки. Причем, эту дискретность в общем случае следует определять непосредственно для тех характерных условий, которые реально определяют моделируемый процесс. В качестве показателя дискретности было выбрано количество узлов на диаметр при моделировании затвердевания цилиндра диаметром 45 мм в песчаной форме. Последовательно измельчая сетку, фиксировали время конца затвердевания цилиндра, которое использовалось в качестве критерия результата расчета. Очевидно, что при недостаточно мелкой разбивке расчет будет давать неверные результаты, которые будут все ближе приближаться к тому решению, которое в состоянии обеспечить данный алгоритм. Когда результаты расчетов перестанут изменяться, можно будет констатировать, что та дискретность при которой перестали происходить изменения результатов и определяет минимально допустимое количество узлов по толщине отдельных фрагментов геометрии. Результаты этих расчетов представлены на рис.5. В данном случае не важно какое время затвердевания дает тот или иной метод (это будет обсуждено ниже), а важно при каком количестве узлов значение этого времени перестает меняться. Из рис.5 видно, что результаты расчета при МКЭ очень быстро приблизились к «окончательным», практически сразу при переходе с 5 до 7 узлов на диаметр и перестали меняться начиная с 8-9 узлов на диаметр. Для МКР же для приближения к «окончательному» результату надо не менее 30 узлов на диаметр, а для достижения практического отсутствия перемен необходимо около 35 узлов. Из общих соображений по кинетике затвердевания и охлаждения можно предположить, что вероятно такая дискретность нужна для фрагментов типа «цилиндр», а для «стенок» она может быть в половину меньше, т.е. 3-4 для МКЭ и 10-15 для МКР. В то же время для фрагментов типа «шар» дискретность видимо должна быть не менее 10-12 узлов для МКЭ и 35-40 для МКР. В МКЭ достижение дискретности в 7-9 узлов по толщине каждого «цилиндрического» фрагмента и 3-4 узла в «стенках» не представляет затруднений и вполне вписывается в ресурсы порядка 50-150 Мб оперативной памяти. Для МКР же, вероятнее всего, достижение требуемой дискретности возможно только для отливок с крайне простой конфигурацией. В противном случае, будет требоваться оперативная память порядка тысяч Мб. Это легко подсчитать, если предположить, что как упоминалось выше, что в МКР на отливку обычно приходиться около сотни узлов по каждой оси. Тогда, несколько утрируя, можно заметить, что отливка с тремя цилиндрическими прибылями по 30 узлов по диаметру каждой прибыли, почти полностью исчерпывают возможности МКР по сложности моделируемой геометрии. Это конечно не совсем так, т.к. вероятно в разностных системах практически никогда не считают с той дискретностью, которую реально требует применение МКР для моделирования ЛП.
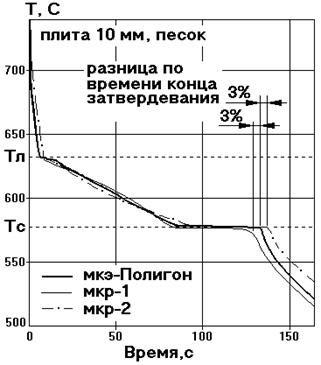
Рис.6 Расчетные температурные кривые для МКЭ и МКР
при затвердевании плиты 10 мм в песчаной форме
Теперь, когда требуемая дискретность обоих методов определена, рассмотрим задачу о определении величин систематических ошибок МКР для конфигураций, отличающихся от «плиты». Как уже указывалось выше, для тел типа «плита» расположенной параллельно одной из плоскостей разностной разбивки, МКЭ и МКР должны давать одинаковые результаты. Сравнительные расчеты показали, что это положение выполняется (см. рис.6). Из рис.6 видно, что разница между МКЭ и МКР по времени конца затвердевания не превышает 3%. Это свидетельствует о том, что все три системы –«МКЭ-Полигон», «МКР-1» и «МКР-2» не содержат не выявленных погрешностей, используют относительно сходные физические модели, а кроме того, что при вводе исходных данных соблюдается их идентичность (одинаковость) для каждой из систем.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.