Однако, основная разница между МКЭ и МКР отнюдь не в разной точности описания геометрии. С точки зрения адекватности решения, основная разница заключается в тех исходных посылках на которых базируется каждый из этих методов. Не углубляясь в математические тонкости формулировки методов, можно с определенной степенью вульгаризации сказать, что МКЭ предполагает некоторое распределение искомой функции внутри элемента, а МКР предполагает ее постоянное значение внутри ячейки. Таким образом, если говорить о распределении температуры по толщине некоторой стенки, то в МКЭ оно описывается непрерывной линией, состоящей из соединенных отрезков, а в МКР ступенчатым профилем. Эти два вида аппроксимации показаны на рис. 2, из которого видно, что при одинаковом шаге дискретизации, МКЭ гораздо точнее описывает реальное температурное распределение, чем МКР. Собственно именно то, что МКЭ в рамках исходных посылок более точно соответствует физике решаемых задач, в которых чаще всего предполагается непрерывное гладкое распределение искомой функции, и делает его более «сильным» методом, чем МКР.
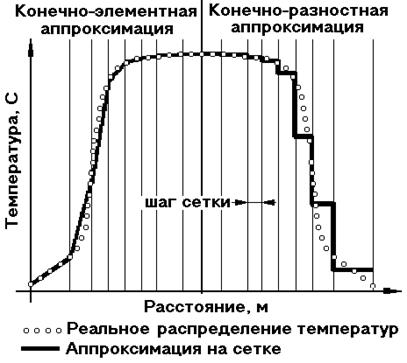
Рис.2 Различная аппроксимация искомой функции при МКЭ и МКР
Следует понимать, что вышеприведенные формулировки не претендуют на строгость и сделаны для упрощения изложения сути. В МКЭ, как уже было сказано выше, не обязательно применять линейную аппроксимацию, тогда температурное распределение будет описываться не набором прямых отрезков, а некоторой линией, состоящей из криволинейных участков. Однако, в «элементных» СМ ЛП чаще всего используются симплекс-элементы, предполагающие именно линейную аппроксимацию. Что касается МКР, то постоянное значение функции в рамках разностной ячейки явно присутствует лишь в «классической» формулировке метода. В различных вариациях МКР, предположение о постоянном значении функции может не присутствовать в явном виде, однако при внимательном анализе его обычно всегда можно обнаружить как неявное предположение при некоторых операциях (чаще всего связанных с теплосодержанием ячейки) или как следствие других исходных посылок. Также не следует путать визуализацию расчетных полей и сам расчет. При применении МКР часто визуализируют температурные поля таким образом, что видно распределение температуры внутри ячейки. Сделать это несложно, например посчитав температуру в каждой вершине ячейки как среднюю от всех ячеек сходящихся в этой вершине, тогда в каждой из 8 вершин ячейки будет своя температура и, соответственно, можно назначить некоторое распределение внутри ячейки. Это безусловно весьма полезный прием, однако он не влияет на характеристики самого расчета, а является постпроцессорной интерпретацией его результатов.
Исходя из выше изложенного, следует сделать вывод о том, что каждый из методов – МКЭ и МКР для достижения правильных результатов расчета предъявляет свои определенные требования к густоте расположения узлов внутри тела помимо тех, которые связаны с точностью описания геометрии. Можно предположить, что количество узлов для МКР должно быть существенно большим, чем для МКЭ. При этом, требуемая густота, как и другие параметры, очевидно будут зависеть от особенностей распределения искомой функции и, таким образом, будут разными для разных процессов и разными для разных условий протекания процесса. Например, для тепловой задачи применительно к ЛП такие параметры могут существенно отличаться от параметров для тепловой же задачи применительно например к работе радиаторов различных механизмов. При этом наиболее важным вопросом будет являтся вопрос о том достижимы ли в реальности те параметры, которые обеспечат адекватное решение для ЛП. (Конкретные значения таких параметров попробуем определить ниже.)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.