Метод наименьших квадратов. Определение параметров эмпирических формул по способу наименьших квадратов в случае линейной зависимости

Метод наименьших квадратов

Наиболее распространенным критерием малости уклонений является критерий, лежащий в основе метода наименьших квадратов: параметры функции ф(х) выбрать так, чтобы оказалась минимальной сумма квадратов уклонений

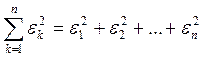
Пусть функция—многочлен степени т, т.е.

Задача параболического приближения функций по способу наименьших квадратов ставится следующим образом: подобрать коэффициенты многочлена так, чтобы сумма квадратов погрешностей для данного т оказалась минимальной.

Если             ,  существует бесконечное множество полиномов,  для   которых  выполняется равенство

.

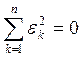В  случае т = п-1 указанное равенство обеспечивается единственным полиномом, дающим решение интерполяционной   задачи.   Если   m<n—1   (в дальнейшем будем рассматривать только этот случай), то

.

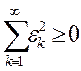при любых значениях коэффициентов полинома ; нужно так выбрать коэффициенты этого полинома, чтобы величина

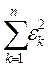стала минимальной.

Отметим, что чем меньше m, тем проще эмпирическая формула, однако понижение степени полинома приводит к увеличению соответствующего минимума суммы квадратов уклонений, следовательно, и самих уклонений.

В следующих параграфах рассмотрим подробнее случаи т=1 и т = 2, т. е. линейное и квадратичное приближения функций по способу наименьших квадратов.

§ 1. Определениепараметровэмпирическихформул

поспособунаименьшихквадратов

вслучаелинейнойзависимости

В естествознании, в частности химических, физических и других науках, приходится пользоваться эмпирическими формулами, составленными на основании результатов опыта и наблюдения. Способ наименьших квадратов — один из наилучших методов получения таких формул. Изложим идею этого способа для случая линейной зависимости двух величин.

Пусть необходимо установить зависимость между двумя величинами хну.Производим п измерений и результаты заносим в таблицу

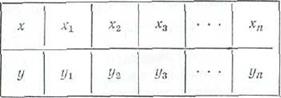
Будем рассматривать и как прямоугольные декартовы координаты точек на плоскости:

.

Предположим, что эти точки почти лежат на некоторой прямой (рис. 20). Естественно в этом случае предположить, что между х и у существует линейная зависимость, т. е. у есть линейная функция от х, выражающаяся формулой

у = ах-\-Ь,(1)

где а н b— некоторые постоянные коэффициенты (параметры), подлежащие определению. Равенство (1) можно записать также в виде

ах-\-Ь~ у^О.(2)

Поскольку точки Mi(xuуг) только приблизительно лежат на прямой, определяемой уравнением (1) или (2), то и формулы эти являются приближенными. Следовательно, подставляя в формулу (2) вместо х и у их значения Xi, Уг (г=1, 2, ..., п), взятые из данной таблицы, получаем равенства:

~у2- е₂;

где 8ь 82, .... е_п — уклонения.

Требуется подобрать коэффициенты а и bтак, чтобы уклонения были по возможности малыми по абсолютной величине. Согласно способу наименьших квадратов, подберем коэффициенты а и bтак, чтобы сумма квадратов уклонений

«-e»+eJ+...-+el  (4)

была наименьшей. Если эта минимальная сумма окажется достаточно малой, то тогда и сами уклонения будут малыми по абсолютной величине.

Подставляя равенства   (3)  в формулу  (4), получаем

и= {ах_{+Ь-1ц)*+ {ах_г-\-Ь~у_г)²+ . .. +(ах_п+Ь—у_п)².

(5)

Переменная величина и является функцией двух переменных а и b(а и Ъ — неизвестные, подлежащие определению; Xi, tji— числа, полученные в результате измерений), Подберем параметры а и bтак, чтобы функция и получила возможно меньшее значение. Для этого необходимо, чтобы

да              ди

= 0,    — =0.                             (6)

да

Находя частные производные функции и по а и Ь, при равнивая их нулю, получаем так называемую нормаль ную систему

(7)

Xi~\-bn =

Из системы (7) определяют параметры а и bэмпирической формулы (1).

Замечание 1. Легко видеть, что если результаты измерений в точности удовлетворяют линейному закону (y=ajc+&), то первые разделенные  разности   (см.  §  2  гл.   IV)   должны  быть  постоянны: