Учебно-методическое пособие для проведения тестирования по дисциплине «Математика». Часть II

Министерство образования Республики Беларусь

Учреждение образования «Гомельский государственный

технический университет имени П.О.Сухого»

Кафедра «Высшая математика»

Н.Н. Бородин, В.И. Гойко, Е.А. Дегтярёва

Учебно-методическое пособие

для проведения тестирования

по дисциплине «Математика». Часть II

 для студентов заочного отделения

Гомель 2012

СОДЕРЖАНИЕ

1.	НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ		5
	1.1	Непосредственное интегрирование	5
	1.2	Метод занесения под знак дифференциала	6
	1.3	Метод замены переменной в неопределенном интеграле	7
	1.4	Метод интегрирования по частям	9
	1.5	Интегрирование выражений, содержащих квадратный трехчлен	11
	1.6	Интегрирование рациональных функций	12
	1.7	Интегрирование иррациональных выражений	15
	1.8	Интегрирование выражений, содержащих тригонометрические  функции	16
	1.9	Универсальная тригонометрическая подстановка	18
2.	ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ		19
	2.1	Понятие определенного интеграла	19
	2.2	Геометрические приложения определенного интеграла	21
3.	ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ		25
	3.1	Основные понятия функции двух и более переменных	25
	3.2	Частные производные первого порядка. Полный дифференциал	27
	3.3	Частные производные высших порядков	29
	3.4	Дифференцирование сложных функций	30
	3.5	Неявные функции и их дифференцирование	32
	3.6	Экстремум функции нескольких переменных. Необходимые и достаточные условия существования экстремума	33
4.	ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ		35
	4.1	Уравнения с разделяющимися переменными	35
	4.2	Однородные уравнения первого порядка	37
	4.3	Линейные уравнения первого порядка. Уравнение Бернулли	39
	4.4	Уравнения в полных дифференциалах	41
	4.5	Дифференциальные уравнения высших порядков. Понижение порядка	42
	4.6	Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами	44
	4.7	Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами	46
	4.8	Системы дифференциальных уравнений	48
	ВАРИАНТЫ ТЕОРЕТИЧЕСКИХ ТЕСТОВЫХ ЗАДАНИЙ		49
	ВАРИАНТЫ ПРАКТИЧЕСКИХ ТЕСТОВЫХ ЗАДАНИЙ		54
	ЛИТЕРАТУРА		59

1. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

1.1 Непосредственное интегрирование

 Функция F(x) называется первообразной для функции f(x) на интервале (a;b), если

а) F(x) дифференцируема на (a;b),

б).

Если F(x) является первообразной для функции f(x) на (a;b), то и любая функция , также является первообразной для f(x) на (a;b).

Неопределенным интегралом от функции f(x) на (a;b) называется множество всех первообразных функции f(x) на этом интервале. Неопределенный интеграл обозначается символом . Неопределенный интеграл записывают в виде формулы:

, (1.1)

где  – любая из первообразных для функцииf(x) на (a;b), С – произвольная постоянная.

Свойства неопределенного интеграла:

1)  

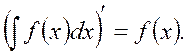
2)  

3)  

4)  

Таблица основных неопределенных интегралов:

I. 

II.  .

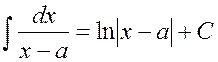III.  .

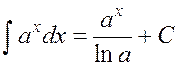IV.  .

V.  .

VI.  .

VII.  .

VIII.  .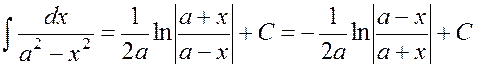

IX.  .

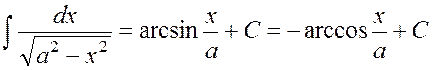X.  .

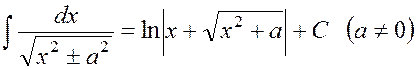XI.  .

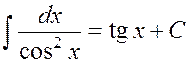XII.  .

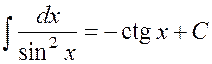Метод непосредственного интегрирования состоит в сведении заданного интеграла к сумме или разности табличных интегралов путем тождественных преобразований подынтегральной функции.

Пример 1.1 Найти .

Решение. Преобразуем подынтегральное выражение:

.

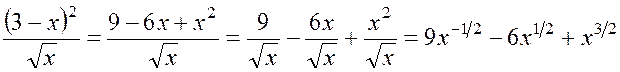Таким образом, получаем:

.

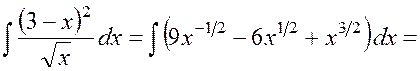
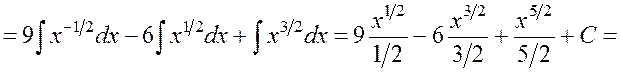
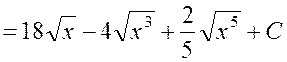Ответ: .

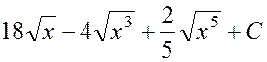1.2 Метод занесения под знак дифференциала

Метод занесения под знак дифференциала основан на определении дифференциала функции одной переменной:

 (1.2)

и свойстве инвариантности дифференциала первого порядка: если , то

. (1.3)

В силу этого свойства, таблица интегралов оказывается справедливой, независимо от того, является ли переменная интегрирования независимой переменной или дифференцируемой функцией.

Пример 1.2 Найти .

Решение. Применим метод занесения под знак дифференциала, воспользовавшись формулой (1.3):

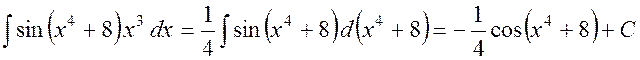
Ответ: .

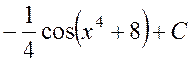1.3 Метод замены переменной в неопределенном интеграле

Метод замены переменной заключается в том, что в интеграле, нахождение которого затруднительно, вводят новую переменную . При этом необходимо, чтобы полученный интеграл  стал табличным или, по крайней мере, был бы ясен способ его нахождения. После вычисления  следует вернуться к исходной переменной.

Пример 1.3 Найти .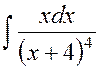

Решение. Подстановкой  знаменатель упрощается, и интеграл приводится к табличным интегралам:

 

.

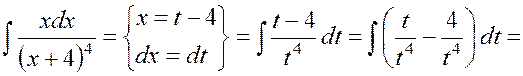
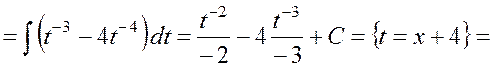
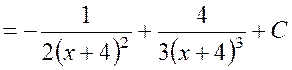Ответ: .

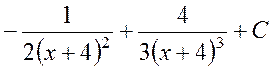Тригонометрические и гиперболические подстановки

Часто для вычисления интегралов, содержащих радикалы вида  применяются тригонометрические и гиперболические подстановки.

1) Если интеграл содержит, то используем следующую замену:  (1.4)

Пример 1.4 Найти .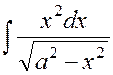

Решение. После применения  тригонометрической подстановки  получим

.

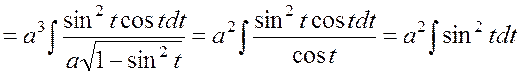Для вычисления полученного интеграла воспользуемся формулой:

.

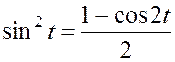Тогда

.

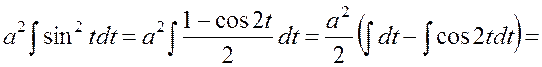
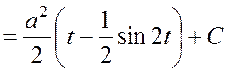Для того, чтобы вернуться к исходной переменной, необходимо провести следующие преобразования:

.

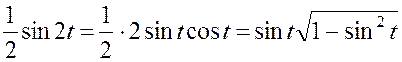Учитывая, что ;

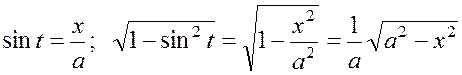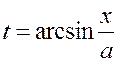; , окончательно получаем:

.

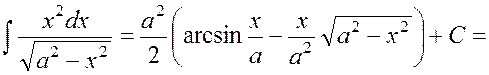
2) Если интеграл содержит радикал , то полагают

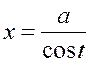. (1.5)

Следует отметить, что часто, полученный  в результате указанной подстановки интеграл, в свою очередь, оказывается довольно сложным. В таком случае можно вместо подстановки (1.5) воспользоваться гиперболической подстановкой

. (1.6)

При использовании гиперболических подстановок надлежит помнить, что

, .

3) Интеграл, содержащий радикал  может быть упрощен путем замен или .

1.4 Метод интегрирования по частям

Метод интегрирования по частям основан на применении формулы

, (1.7)

где  – непрерывно дифференцируемые на некотором интервале функции.

К интегралам, которые находят методом интегрирования по частям, относятся интегралы следующих видов:

1) , где  – полином n-ой степени от x.

В данном случае за  следует выбрать , а за  –  или .

Таким образом, в результате применения формулы (1.7) мы пришли к интегралу более простому по отношению к исходному. Следует подчеркнуть, что формула интегрирования по частям может быть применена несколько раз, до тех пор, пока мы не придем к , т.е. не придем к интегралу .

2) , где  – полином степени n от x.

В данном случае за  обозначают , за . Формула интегрирования по частям применяется до тех пор, пока не останется .

3) .

В данном случае за  следует выбирать ; ; , за . Тогда в результате применения формулы интегрирования по частям мы приходим к интегралам, содержащим только рациональные функции и радикалы.

4) Интегралы вида  вычисляются с помощью двукратного применения формулы интегрирования по частям и последующего решения полученного уравнения относительно исходного интеграла. Следует отметить, что в данном случае безразлично, что изначально принимать за , а что за .

Пример 1.5 Найти .

Решение.

.

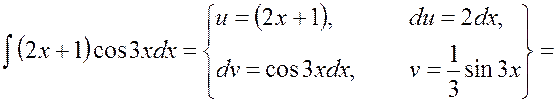
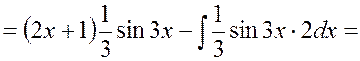
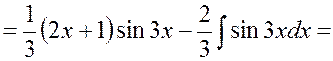
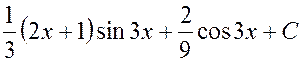Пример 1.6 Найти .

Решение.

.

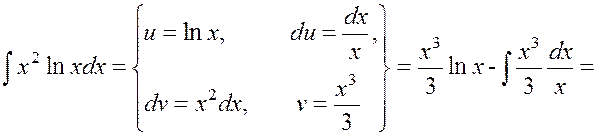
1.5 Интегрирование выражений, содержащих квадратный трехчлен

Интегралы вида 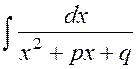 и 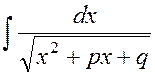 после выделения полного квадрата в квадратном трехчлене сводятся к одному из табличных интегралов вида VII, VIII, IX или X.

Пример 1.7Найти .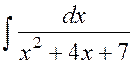

Решение.

.

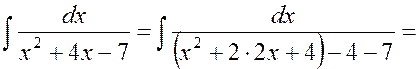
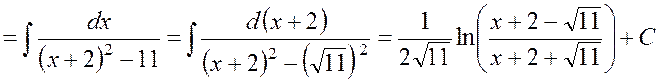Ответ: .

Для вычисления интеграла вида 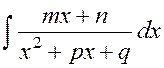 необходимо выделить производную знаменателя в числителе подынтегральной функции:

, .

Тогда исходный интеграл преобразуется в сумму двух интегралов

.

Интеграл  найдем методом занесения под знак дифференциала , интеграл  сводится к табличным интегралам (предварительно выделяя полный квадрат в знаменателе).

Таким образом,

. (1.8)

Пример 1.8 Найти .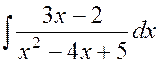

Решение. Найдем . Выделим  в числителе функции: .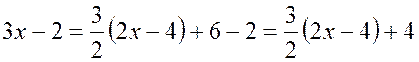

Таким образом

,

,

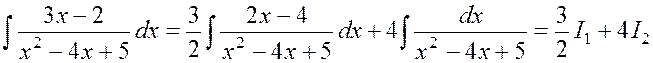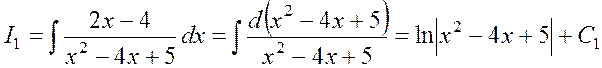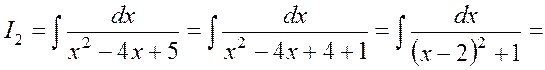{табличный интеграл типа VII}.

Ответ: .

1.6. Интегрирование рациональных функций

Функция, заданная в виде

,

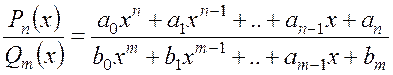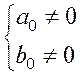
называется рациональной функцией.

Если , то дробь правильная, при  – дробь неправильная.

Метод интегрирования правильной рациональной дроби состоит в разложении этой дроби на простейшие. При этом следует пользоваться следующим правилом:

а) если множитель  входит в разложение  только в первой степени, мы поставим ему в соответствие единственную простую дробь:

;

б) если в разложение  входит множитель , то есть показатель степени , то ему соответствует сумма из  простых дробей:

 ;

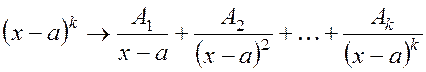в) если в разложение  входит множитель  только в первой степени, то в соответствие ему ставится единственная простая дробь:

 ;

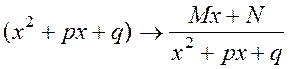г) если в разложение  входит множитель , показатель которого , то ему соответствует сумма из  простых дробей

.

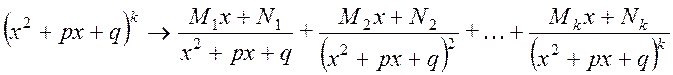Итак, общее правило интегрирования рациональных дробей:

1. Если дробь неправильная, то представить её в виде суммы многочлена и правильной дроби.

2. Разложить знаменатель правильной рациональной дроби на множители.

3. Представить дробь в виде суммы простейших рациональных дробей.

4. Найти неизвестные коэффициенты способом сравнения соответствующих коэффициентов или способом частных значений (см. пример ниже).

5. Проинтегрировать многочлен и полученную сумму простейших дробей.

Пример 1.9 Разложить дробь 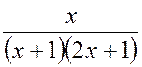 на простейшие.

Решение. .

Найдём коэффициенты  и .

1 способ – метод неопределённых коэффициентов:

.

Приравняем коэффициенты при  и  в обеих частях полученного равенства

 .

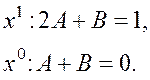
2 способ – метод частных значений:

.

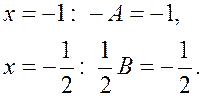
Ответ: .

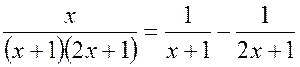Пример 1.10 Найти .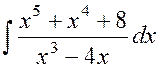

Решение. Подынтегральная функция есть неправильная рациональная дробь (степень числителя больше степени знаменателя), которую сначала представим в виде суммы многочлена и правильной рациональной дроби, разделив числитель и знаменатель по правилу «деления углом»:

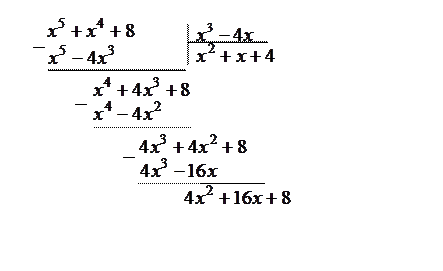
Следовательно,

.

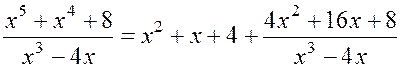Для представления правильной дроби 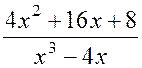 в виде суммы простейших дробей преобразуем её знаменатель следующим образом:

.

Таким образом, полученную правильную дробь можно представить в виде суммы простейших дробей:

.

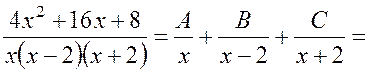
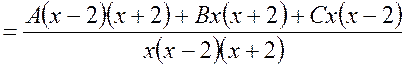Отсюда получаем

.

Найдём коэффициенты , ,  методом частных значений. Подставляя поочерёдно значения , , , получаем

.

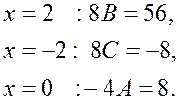
Итак,

.

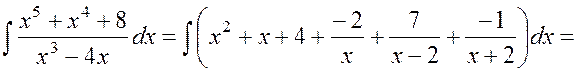
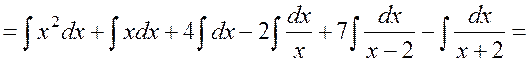
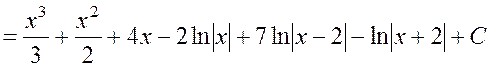Ответ: .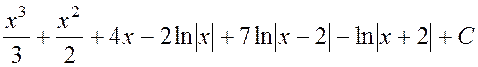

1.7 Интегрирование иррациональных выражений

I.Интегралы вида

 сводятся к интегралам от рациональной функции с помощью подстановки , где k – наименьшее общее кратное чисел .

II. Интегралы вида

рационализируется подстановкой: 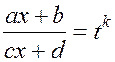, где k – наименьшее общее кратное чисел .

Пример 1.11 Найти .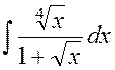

Решение. Т.к. наименьшее общее кратное чисел 4 и 2 равно числу 4, то делаем подстановку

, .

Получаем:

.

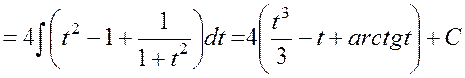Возвращаясь к переменной , получим

.

Ответ: .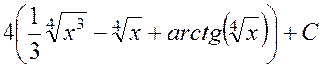

1.8 Интегрирование выражений, содержащих тригонометрические  функции

I. Интегралы вида

 (1.9)

находят, применяя различные тригонометрические формулы в зависимости от значений m и n.

1) хотя бы одно из чисел m и n положительно и нечетно. Пусть , тогда интеграл (1.9) можно преобразовать следующим образом:

.

Аналогично поступают в случае .

2) оба числа m и n – четные и положительные (или нуль). В этом случае степени в подынтегральной функции понижают с помощью формул:

.

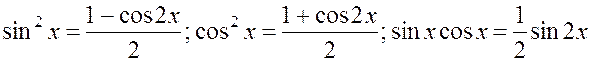3) если . В этом случае подынтегральная функция записывается в виде дроби, в знаменателе которой выделяется множитель  (или ). Выражение 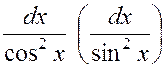 заменяем на  и делаем замену .

Пример 1.12 Найти .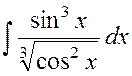

Решение. По условию одна из степеней нечетная, поэтому можно записать

.

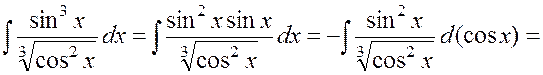
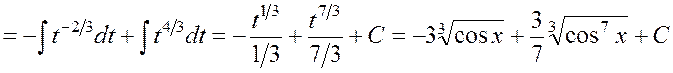Ответ: .

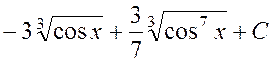Пример 1.13 Найти .

Решение. Для вычисления интеграла применим формулу понижения степени:

.

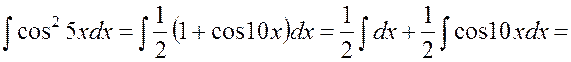
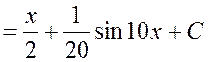Ответ: .

Пример 1.14 Найти .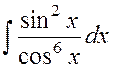

Решение. Здесь , поэтому полагаем:

, , .

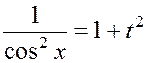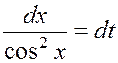Следовательно

.

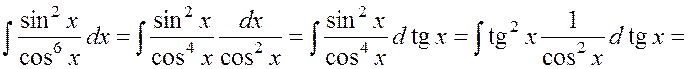
Ответ: .

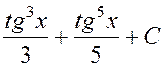II. Интегралы вида

преобразуются с помощью тригонометрических формул

.

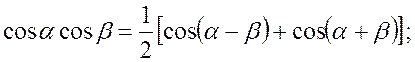
Пример 1.15 Найти .

Решение.

.

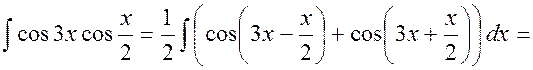
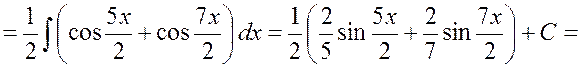
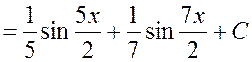Ответ: .

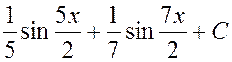III. В интегралах вида:  (или ) где m – целое положительное число, применяется подстановка  (или ).

Пример 1.16. Найти .

Решение. Сделаем подстановку , 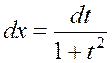. Тогда

.

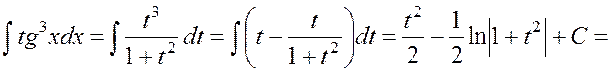
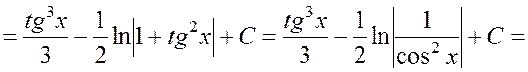
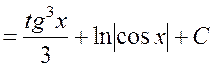Ответ: .

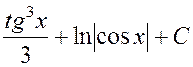1.9 Универсальная тригонометрическая подстановка

Интегралы вида  где – рациональная функция, аргументами которой являются  и , в общем случае приводятся к интегралам от рациональных функций