Метод наименьших квадратов. Определение параметров эмпирических формул по способу наименьших квадратов в случае линейной зависимости, страница 2

Если же линейная функция лишь приближенно отражает существующую зависимость, выписанные равенства заменяются приближенными равенствами.

Следовательно, эмпирическая формула у=ах-\-Ь окажется пригодной лишь в случае, когда первые разделенные разности мало отличаются Друг от друга.

Отметим, что в тех случаях, когда таблица результатов измерений имеет постоянный шаг, т. е. значения аргумента образуют арифметическую прогрессию: x* = X(+(A~l)A, достаточно сравнить неразделенные разности &Уь.=*уъ.+г—Ук (см. § 2 гл. IV).

Установить вид зависимости между этими величинами и найти параметры эмпирической формулы.

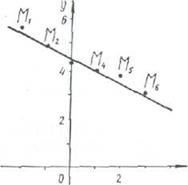
Будем считать, что соответствующие пары значений (Xi, yi), где i = l, 2, ..., 6,— прямоугольные декартовы координаты некоторых точек плоскости. Построим точки Mi{—2; 5,6), Ah(—1,5), Мз(0; 4,3), М_А(1А), М₅(2; 3,6), УИб (3,3) относительно прямоугольной декартовой системы координат (рис. 21). Эти точки располагаются приблизительно на некоторой прямой (см. рис. 21), уравнение которой может быть записано в виде у = ах-\~Ь, Следовательно, можно предположить, что между величинами х и у существует линейная зависимость у = ах-\-Ь, где а и b — неизвестные коэффициенты. Определим параметры а и bэмпирической формулы у = = ах-\-Ь, использовав нормальную систему уравнений (7). В этой системе коэффициентами при неизвестных а

и Ь являются суммы полученных опытным путем значений Xi, yi, их произведений хф, квадратов значений первой величины   (**). Число проведенных измерений равно п.

Чтобы найти эти коэффициенты, необходимо подсчитать указанные суммы. Результаты измерений х, у и итоги их обработки представлены в таблице (табл. 1).

. Определение параметров эмпирических формул по способу наименьших квадратов в случае квадратичной зависимости

В   результате   измерений   двух   зависимых   величин х и у получена следующая таблица их значений:

Рассматриваем пары значений (x_ity_t) как прямоугольные декартовы координаты точек на плоскости. Предположим, что точки с соответствующими координатами Mi (Xi, yi), М_г (х₂, уг), ..., ..., М_п (х_п> Уп) почти лежат на некоторой параболе (рис. 22). В этом случае естественно предположить, что между х и у существует квадратичная    зависимость,

i = ax²+bx+c,       (8)

где а, Ъ, с — постоянные коэффициенты, подлежащие определению.

Если в правую часть формулы (8) вместо х подставить значения x_tиз данной таблицы, получим числа

Zi=ax\+bxi-\-c.      (9)

Было бы идеальным подобрать параметры а, Ь, с так, чтобы при всех izi — yi(/=1, 2, 3, ..., п).Однако при /г>3 этого обычно сделать не удается, так как значения а, Ь, с, найденные из уравнений: yi — euP+bxi+c, y₂

-\-с, у₃ = ах²_з-\-Ьх₃-\-с,  как правило, не будут удовлетворять уравнениям   у^ = ах^-\-Ьх^~\-с,. . ., у_п = ах² -\-Ьх_п-\-с,

если у(х) не была квадратным трехчленом. Другими сло-I     вами,

:                             Zi—yi = zi(1=1,2,3, ...,п),                 (10)

₍      где 8г — уклонения.

,_г                  Параметры формулы   (8)  выберем так, чтобы сумма квадратов уклонений

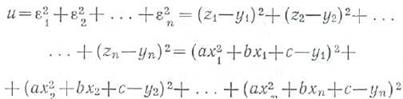
наименьшей. Для этого необходимо, чтобы

да да

Находя выражения для частных производных функции по переменным а, Ь, с, получаем нормальную систему уравнений

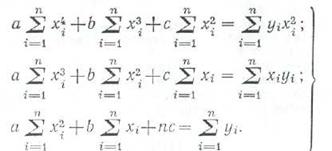
Из системы (12) определяются параметры а, Ь, с эмпирической формулы (8). Решение системы (12) осуществляется методами, рассмотренными в гл. I.

Замечание 3. Эмпирическая формула у=ах²-{-Ьх-\-с оказывается пригодной в случае, когда мало отличаются друг от друга разделенные разности второго порядка. Если Xk=X\-\-(k~\)h, то сравнивают неразделенные разности второго порядка Д²(/а = Лг/й+1—