Пусть функция y=f(x) определена в точке х0 и в некоторой окрестности этой точки. Функция y=f(x) называется непрерывной в точке х0, если существует предел функции в этой точке и он равен значению функции в этой точке:
Это означает:
- функция определена в точке х0 и в ее окрестности;
- функция имеет предел при х→х0
- предел функции в точке х0 равен значению функции в этой точке, т.е. выполняется равенство.
Это означает, что при нахождении предела непрерывной функции f(x) можно перейти к пределу под знаком функции, то есть в функции f(x) вместо аргумента х подставить предельное значение х0
8 1 замечательный предел и др. замечательные пределы:
1 замечательный предел.
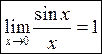
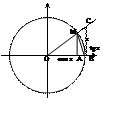
Возьмем круг радиуса 1, обозначим радианную меру угла MOB через Х.
Пусть 0 < X < π/2. На рисунке |АМ| = sin x, дуга МВ численно равна центральному углу Х, |BC| = tg x. Тогда
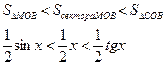
Разделим все на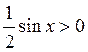 
и получим:
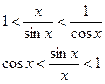
Т.к. 
,
то по признаку существования пределов следует 
.
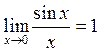2 замечательный предел.
Пусть х→∞. Каждое значение х заключено между двумя положительными целыми числами:
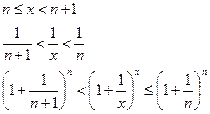
Если x→∞, то n→∞, тогда
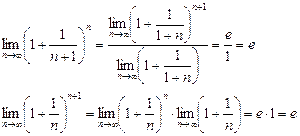
По признаку о существовании пределов:
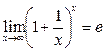
9 Классификация точек разрыва:
Точки разрыва функции – это точки в которых нарушается непрерывность функции.
Точка разрыва х0 называется точкой разрыва 1 рода функции y=f(x), если в этой точке существуют конечные пределы функции слева и справа (односторонние пределы)
и 
При этом, если:
- А1=А2 то точка х0 называется точкой устранимого разрыва;
- А1≠А2 то точка х0 называется точкой конечного разрыва.
|A1 – A2| называется скачком функции.
Точка разрыва х0 называется точкой разрыва 2 рода функции y=f(x), если по крайней мере один из односторонних пределов (слева или справа) не существует, либо равен бесконечности.
10 Производная геометрический смысл производной:
Смысл производной - это скорость изменения ф-ции при изменении аргумента.
y=f(x+Dx)-f(x), y=f(x). производной в точке а называется предел отношения приращения ф-ции к приращению аргумента:
lim(Dy/Dx)=lim((f(x+Dx)-f(x))/Dx)=dy/dx
Dx®0 Dx®0
Вычисление производной: lim(Dy/Dx)=y` Dx®0
1) если y=x, Dy=Dx, y`=x=lim(Dy/Dx)=1.
2) если y=x2, Dy=(x+Dx)2-x2=x2+2xDx+Dx2-x2=Dx(2x-Dx),
(x2)`=lim((Dx(2x+Dx))/Dx)=lim(2x+Dx)=2x
x®0 Dx®0
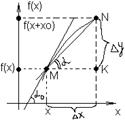
Геометрический смысл производной.
KN=Dy, MK=Dx
DMNK/tg2=Dy/Dx
вычислим предел левой и правой части:
limtga=lim(Dy/Dx) Dx®0
tga0=y`
11 Дифференцируемость функции:
Функция y=f(x), имеющая производную в каждой точке интервала (a;b) называется дифференцируемой в этом интервале.
Операция нахождения производной называется дифференцированием.
Дифференциал функции y=f(x) в точке х называется главная часть ее приращения, равная произведению производной функции на приращение аргумента, и обозначается dy (или df(x) ).
Иначе. Дифференциал функции равен произведению производной этой функции на дифференциал независимой переменной.
Теорема- для того чтобы ф-ия f(x) имела в точке а конечную производную необходимо и достаточно чтобы она была дифференцируема в этой точке.
12 Правило дифференцирования
Теорема: Если f(x) и g(x)
дифферен. в точке х, то: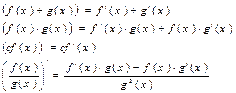 
Теорема о произв. сложной функции:
Если y(x)=f(u(x)) и существует f’(u) и u’(x), то существует y’(x)=f(u(x))u’(x).
Теорема о произв. обратной функции.
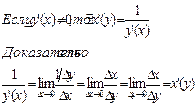
Таблица производных:
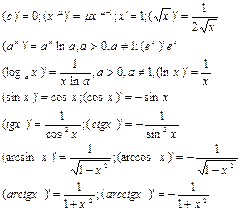
13 Производная обратной ф-ии
Если ф-ия y=f(x) монотонно возр.(уб.) некоторые окрестности точки x0, то в окрест. точки y0=f(x0) опред. обратная функция x=f-1(y)
Пусть функция y=f(x) монотонно возрастает (убывает) в окрестности точки x0 и непрерывна, тогда если y=f(x) дифференцируема в точке x0 и производная в точке x0 не равна 0, то в окрестности точки y0 существует обратная функция, которая дифференц. в точке y0 и ее производная x’(y0)=1/y’(x0)
14. Дифференцирование сложных ф-ций:
Производная сложной ф-ции = произведению производной ф-ции по промежуточному аргументу и производной самого промежуточного аргумента по независимой переменной.
y`=f(x)*U`,или yx`=yU`*Ux`, или dy/dx=dy/dU=dU/dx
Например:
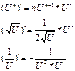
15.Формула Лейбница. n-ая производная:
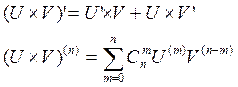
16.Теорема «локальная ограниченность функции имеющей конечный предел»
Т. – если ф-ия f(x) имеет в точке а конечный предел b то в окрестности а найдется некоторая окрестность точки а в пределе которой ф-ия f(x) ограничена
17.Теорема о сохранении знака о неприрывной ф-ии:
Пусть ф-ия f(x) непрерывна в точке а и f(a) <>0 тогда найдется
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
