Численное интегрирование. Вычисление значения интеграла по формулам прямоугольников и Симпсона с точностью e = 0.001

Задание:

Дан интеграл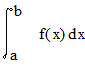      

Вычислить его значение по формулам прямоугольников и Симпсона с точностью e = 0.001, используя правило Рунге, как критерий окончания счета.

|I-I^h/2| » |I^h-I^h/2|/(2^p-1) £ e

I^h/2 – есть ответ.

Вывести значение шага, при котором точность была достигнута.

Априорная оценка для последнего значения h. Исходя из заданного e, вычислить теоретическое значение шага.

Параметры:

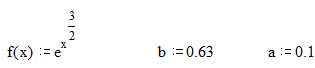
Решение:

1.  Метод прямоугольников.

Процедура для вычисления интеграла по методу прямоугольников с заданным шагом:

(где n=(b-a)h        h- шаг)

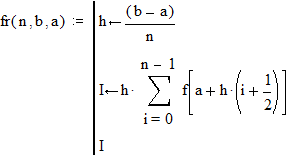
Процедура для вычисления интеграла с заданной точностью D по методу прямоугольников:

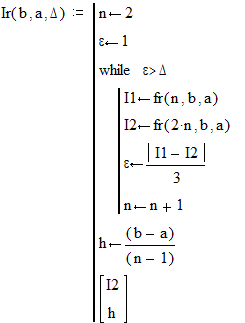
Результат:

Значение интеграла I^h/2:

Значение шага, при к-ром была достигнута заданная точность:

Априорная оценка погрешности:

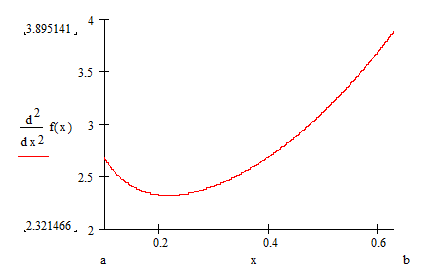
точка максимума b.

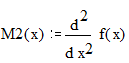
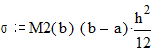
Теоретическое значение шага:

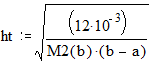
2.  Метод Симпсона.

Процедура для вычисления интеграла по методу Симпсона с заданным шагом:

(где n=(b-a)h        h- шаг)

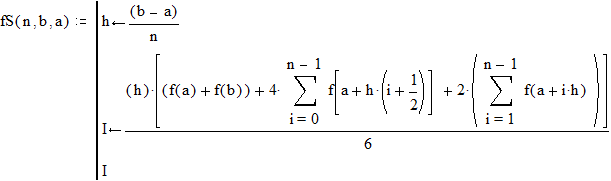
Процедура для вычисления интеграла с заданной точностью D по методу Симпсона:

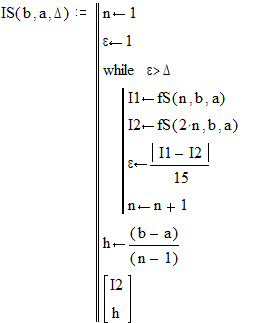
Результат:

Значение интеграла  I^h/2:

Значение шага, при к-ром была достигнута заданная точность:

Априорная оценка погрешности:

           

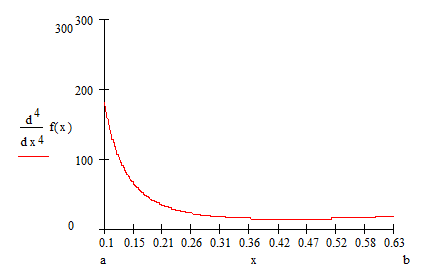
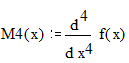
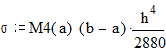
Теоретическое значение шага:

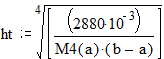
Arthur Dambis. ©