Встановлення закону зміни випадкових величин по результатам вимірів

Національний Технічний Університет України

«Київський Політехнічний Інститут»

РОЗРАХУНКОВО ГРАФІЧНА РОБОТА

з предмету:

«ОСНОВИ НАУКОВИХ ДОСЛІДЖЕНЬ»

ВСТАНОВЛЕННЯ ЗАКОНУ ЗМІНИ ВИПАДКОВИХ

ВЕЛИЧИН ПО РЕЗУЛЬТАТАМ ВИМІРІВ

Виконав:

Студент V курсу ММІ

групи МАм-62

Вороний Г.О.

Провірив:

Шишкін В.М.

Київ 2010

1.  ПОБУДОВА ЕМПІРИЧНОЇ КРИВОЇ

Таблиця відхилень результатів випробування розміру .

Таблиця 1

№	Х	№	Х	№	Х	№	Х
1 2 3 4 5 6 7 8 9 10 11 12 13	+0,005 +0,015 -0,015 -0,025 +0,015 +0,020 -0,022 -0,013 -0,014 -0,012 -0,019 +0,021 -0,018	14 15 16 17 18 19 20 21 22 23 24 25 26	-0,012 -0,012 -0,001 +0,019 -0,020 -0,005 -0,011 -0,016 -0,021 +0,012 -0,012 -0,026 -0,018	27 28 29 30 31 32 33 34 35 36 37 38 39	-0,019 -0,023 -0,012 -0,025 -0,015 +0,020 +0,022 +0,016 -0,016 +0,006 +0,012 -0,002 -0,017	40 41 42 43 44 45 46 47 48 49 50	-0,015 +0,022 -0,018 -0,015 -0,019 -0,004 -0,009 -0,012 -0,013 +0,029 +0,011

Максимальне відхилення: .

Мінімальне відхилення: .

Зона розсіювання: .

Розділимо зону розсіювання на 10 груп, з інтервалом . Підрахуємо число відхилень розмірів, розташованих в кожному інтервалі. Для чого всі значення таблиці 1 занесемо у вигляді умовних позначень у відповідні інтервали.

Таблиця 2

Номер інтервалу	Інтервал		Середина інтервалу	Частоти		Частоти
	від (включно)	до		в умовних позначеннях	у цифрах
1 2 3 4 5 6 7 8 9 10	-0,0260 -0,0205 -0,0150 -0,0095 -0,0040 0,0015 0,0070 0,0125 0,0180 0,0235	-0,0205 -0,0150 -0,0095 -0,004 0,0015 0,0070 0,0125 0,0180 0,0235 0,0290	-0,02325 -0,01775 -0,001225 -0,00675 -0,00125 0,00425 0,00975 0,01525 0,02075 0,02625		6 14 10 3 2 2 3 3 6 1	0,12 0,28 0,20 0,06 0,04 0,04 0,06 0,06 0,12 0,02

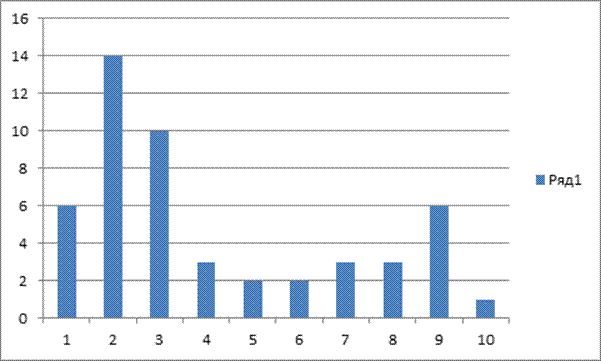
Рис.1                                                          

2. ОБЧИСЛЕННЯ ПАРАМЕТРІВ ЕМПІРИЧНОГО РОЗПОДІЛУ

У випадку, коли значення випадкової величини  задані більш ніж двозначними числами і об’єм вибірки , то розрахунок параметрів доцільно вести шляхом введення нової випадкової величини:

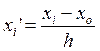
де  – нова випадкова величина;

 – величина інтервалу;

 – деяке початкове значення.

Обчислимо середнє значення, середньо квадратичне відхилення, асиметрію та ексцес.

Розрахунок проведемо на основі даних табл.2. Для цього заповнимо табл.3.

Таблиця 3

№	інтервали	Частоти	Середина інтервалу
1	2	3	4	5	6	7	8	9
1 2 3 4 5 6 7 8 9 10	-0,026-0,0205 -0,0205-0,015 -0,015-0,0095 -0,0095-0,004 -0,0040,0015 0,00150,007 0,0070,0125 0,01250,018 0,0180,0235 0,02350,029	6 14 10 3 2 2 3 3 6 1	-0,023215 -0,01775 -0,01225 -0,00675 -0,00175 0,00425 0,00975 0,01525 0,02075 0,02625	-3,833333 -2,833333 -1,833333 -0,833333 0,166666 1,166666 2,166666 3,166666 4,166666 5,166666	-23 -39,666 -18,333 -2,5 0,333 2,333 6,5 9,5 25 5,166	88,166 112,388 33,611 2,0833 0,0555 2,7222 14,0833 30,0833 104,166 25,694	-337,97 -318,43 -61,62 1,73 0,009 3,17 30,51 95,26 434,02 137,92	1295,56 902,23 112,97 1,44 0,001 3,70 66,11 301,68 1808,44 712,59
Сума		50			-34,66	414,05	-18,85	5204,74

Приймаємо . Тоді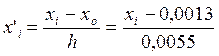  

Визначаємо початкові моменти:

;

;

.

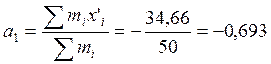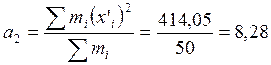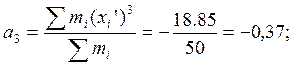
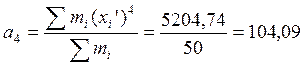Визначаємо центральні моменти:

;

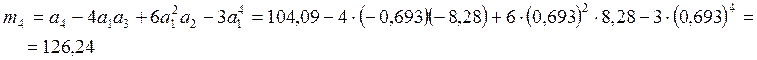
Визначаємо середнє значення та середнє квадратичне відхилення

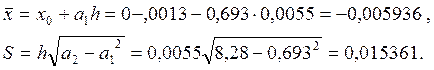
Показник асиметрії: ;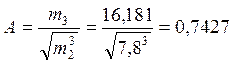

Показник ексцесу: ;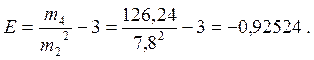

3. ВИЗНАЧЕННЯ ПОЛЯ ДОПУСКУ

Задамося надійністю допуску. Нехай . Задамося можливістю , тобто задаємо площу генеральної кривої, яка входить в допуск. .

По табл.7  знаходимо, що  (, , )

Визначимо границі поля допуску:

;

.

Знайдемо середину та половину поля допуску:

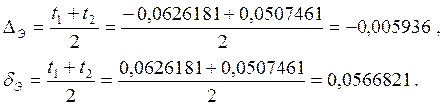
4. ВИЗНАЧЕННЯ КОЕФІЦІЄНТІВ ВІДНОСНОЇ АСИМЕТРІЇ І ВІДНОСНОГО РОЗСІЮВАННЯ

При , ,            , ,       

Тоді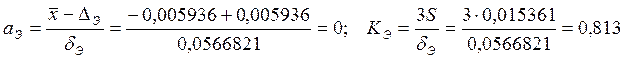

5. ВИРІВНЮВАННЯ ЕМПІРИЧНОГО РОЗПОДІЛУ ЗА ТЕОРЕТИНОЮ ГИПОТЕЗОЮ

Проведемо вирівнювання емпіричного розподілу по нормальному закону Гауса.

Підставимо значення  та  у функцію щільності , замінюючи  на ,  на :

.

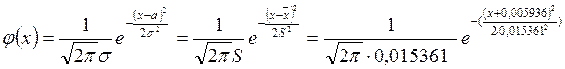Результати вирівнювання приведені у таблиці 4.

Таблиця 4