|
Номер інтервалу |
Середина інтервалу |
Емпіричні частоти |
|
|
|
Ймовірність інтервалів
|
Теоретичні частоти |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
1 2 3 4 5 6 7 8 9 10 |
-0,02325 -0,01775 -0,01225 -0,00675 -0,00125 0,00425 0,00975 0,01525 0,02075 0,02625 |
6 14 10 3 2 2 3 3 6 1 |
-0,017314 -0,011814 -0,006314 -0,000814 0,004686 0,010186 0,015686 0,021186 0,026686 0,032186 |
-1,12714 -0,76909 -0,41104 -0,05299 0,30505 0,66310 1,02115 1,37920 1,73725 2,09530 |
0,2113 0,2968 0,3666 0,3984 0,3808 0,3202 0,2368 0,1540 0,0881 0,0443 |
0,07567 0,10628 0,1313 0,14268 0,13638 0,11466 0,0848 0,05516 0.03156 0,01589 |
3,7834 5,3138 6,5648 7,1338 6,8188 5,7331 4,2399 2,7581 1,5781 0,7943 |
|
Сумма |
52 |
В колонці 5 визначається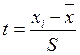 
, де 
– середина 
-го
інтервалу; 
– середнє значення; 
– середньо квадратичне відхилення.
По знайденим 
в
додатку 
знаходимо значення 
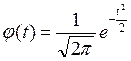
Ймовірність кожного інтервалу (при розрахунках маємо на увазі, що всі значення інтервалів згуртовані в його середині).
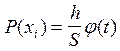, де 
– ширина інтервалу
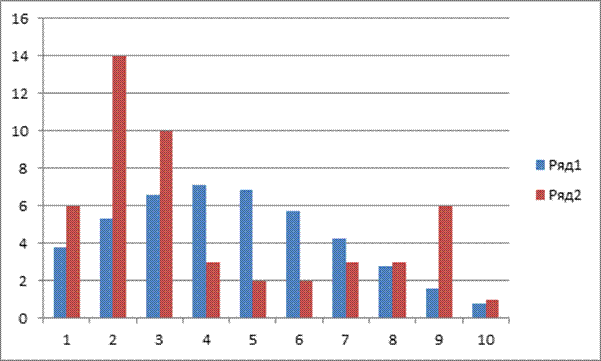
Рис.2. Гістограма емпіричних частот; гістограма вирівняних частот
ПОРІВНЯННЯ ЕМПІРИЧНОЇ ТА ТЕОРЕТИЧНОЇ ФУНКЦІЇ РОЗПОДІЛУ ЗА КРІТЕРІЄМ УЗГОДЖЕНОСТІ
1. Критерій Пірсона
Необхідно об’єднати частоти, що зустрічаються менше 5.
Визначаємо число ступенів вільності 
- число порівнюючих
частот (об’єднанні частоти на кінцях приймаються за одну);
- число параметрів
теоретичної функції розподілення
.
,
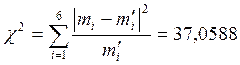тобто криві не узгоджуються.
Таблиця 5
|
Номер інтервалу |
|
|
|
|
|
|||||||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
|||||||||||||||
|
1 2 3 4 5 6 7 8 9 10 |
6 14 30 10 3 2 2 3 3 6 1 |
3,7834 5,3138 15,662 6,5648 7,1338 6,8188 5,7331 4,2399 2,7581 1,5781 0,7943 |
14,3381
4,4219 0,2057 |
205,58111
19,5532 0,0423125 |
13,1261
12,390343 0,0532501 |
|||||||||||||||
|
Сума |
50 |
31,79 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
