Основы деформационной теории пластичности (теория малых упругопластических деформаций)

Основы деформационной теории пластичности

(теория малых упругопластических деформаций)

1. Основные сведения по теории напряжений

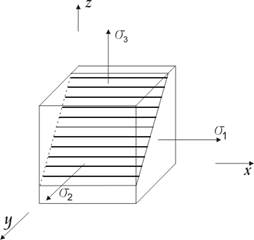
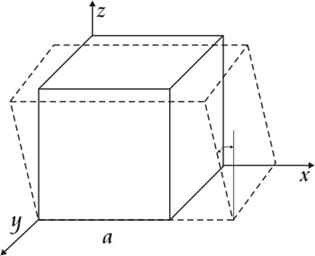
Выделим элементарный объем нагруженного тела в виде параллелепипеда. Тело не обязательно упругое. (!)

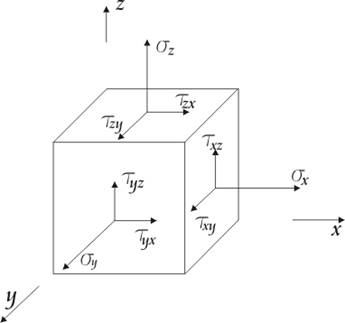
Напряженное состояние характеризуется нормальными напряжениями s_x , s_y , s_z и касательными t_xz , t_xy , t_yz , t_yx , t_zx , t_zy – тензор напряжений.

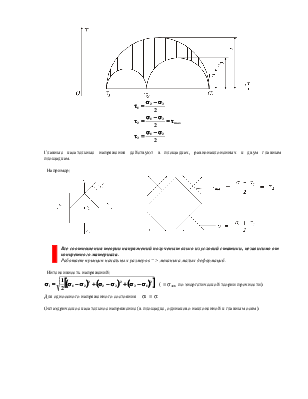
Закон парности касательных напряжений:

t_xz = t_zx

t_xy = t_yx

t_yz = t_zy .

Можно показать, что в каждой исследуемой точке напряженного тела существует такая система осей X, Y, Z, в которой касательные напряжения равны нулю. Другими словами, среди множества осей, которые могут быть проведены через исследуемую точку, существуют три взаимно перпендикулярные оси, в системе которых касательные напряжения отсутствуют. Эти оси называются главными осями напряженного состояния и обозначаются цифрами 1, 2, 3. Нормальные напряжения в направлении этих осей называются главными напряжениями  s₁ => s₂ => s₃ .

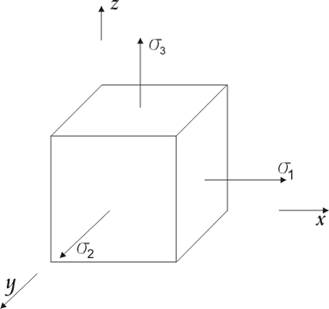
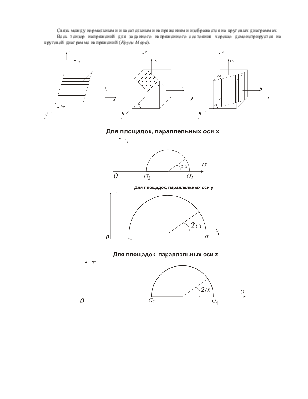
Связь между нормальными и касательными напряжениями изображается на круговых диаграммах.

Весь тензор напряжений для заданного напряженного состояния хорошо демонстрируется на круговой диаграмме напряжений (Круги Мора).

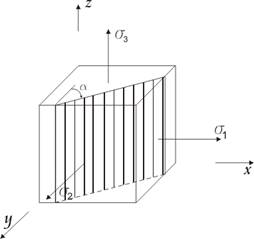
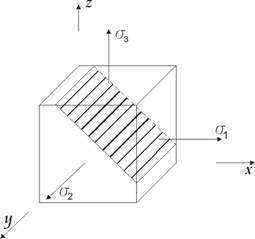
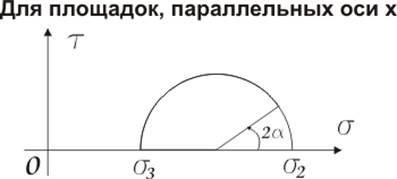
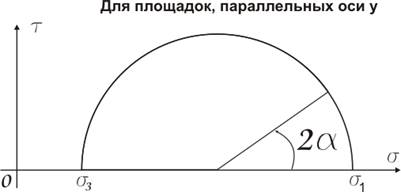
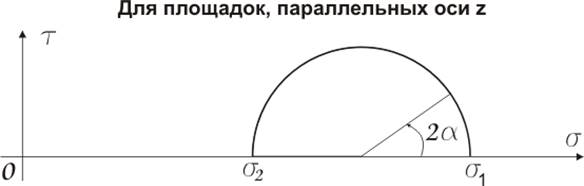
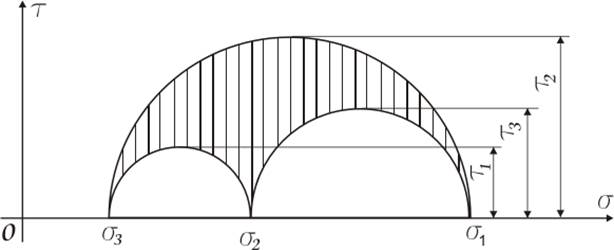
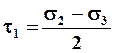
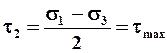
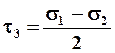
Главные касательные напряжения действуют в площадках, равнонаклоненных к двум главным площадкам.

Например:

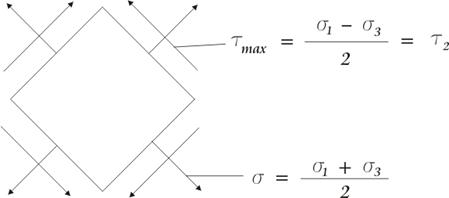
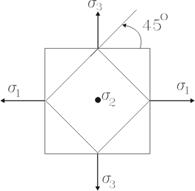
Все соотношения теории напряжений получены только из условий статики, независимо от конкретного материала.

Работает принцип начальных размеров => механика малых деформаций.

Интенсивность напряжений:

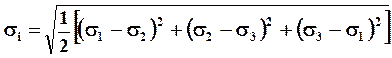   ( = s_экв  по энергетической теории прочности).

Для одноосного напряженного состояния    s_i  = s.

Октаэдрическое касательное напряжение (в площадке, одинаково наклоненной к главным осям).

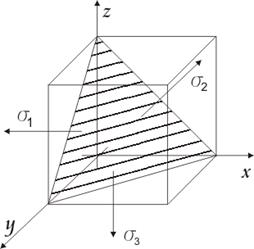
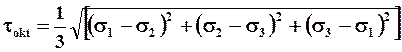
Интенсивность касательных напряжений:

2. Основные сведения из теории деформаций.

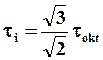
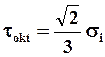
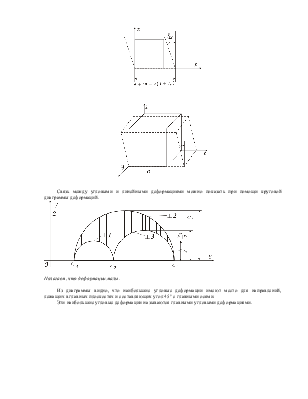
Деформированное состояние напряженного тела характеризуется линейными деформациями e_x , e_y , e_z и угловыми деформациями (углами сдвига) g_xy , g_yz , g_zx .

Среди множества осей, которые могут быть проведены через исследуемую точку, существуют три взаимно перпендикулярные оси, в системе которых угловые деформации отсутствуют, и, следовательно, углы между этими осями при деформации не изменяются. Эти оси называются главными осями деформированного состояния и обозначаются цифрами 1, 2, 3. Линейные деформации в направлении этих осей называются главными линейными деформациями e₁ ³ e₂ ³ e₃ .

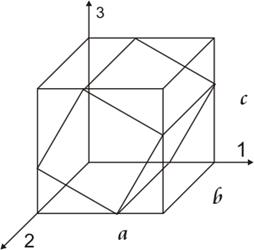
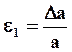
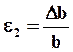
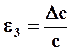
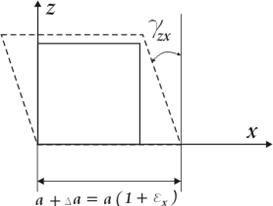
Связь между угловыми и линейными деформациями можно показать при помощи круговой диаграммы деформаций.

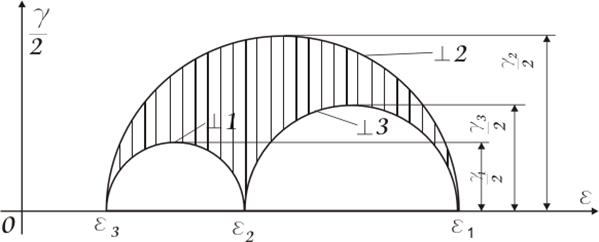
Полагаем, что деформации малы.

Из диаграммы видно, что наибольшие угловые деформации имеют место для направлений, лежащих в главных плоскостях и составляющих угол 45° с главными осями.

Эти наибольшие угловые деформации называются главными угловыми деформациями.

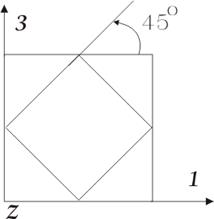
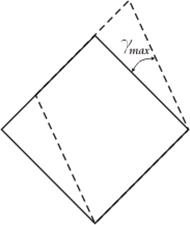
     ( = g_max)

Анализ деформированного состояния основан на чисто геометрических соотношениях. Не зависит от механических свойств материала. Требуется сплошная среда. Механика малых деформаций

Интенсивность деформаций:

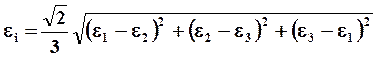
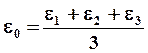Для одноосного состояния: , где   или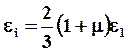

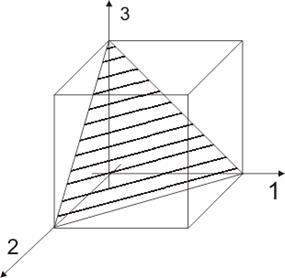
Октаэдрическая угловая деформация (в перпендикулярном направлении, составляющем равные углы с тремя главными осями).

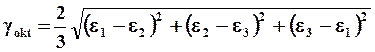
3. Связь между напряжениями и деформациями в упругой стадии.

Для упругого изотропного тела в пределах малых деформаций зависимость между компонентами напряженного и деформированного состояний является линейной и носит название обобщенного закона Гука.

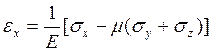
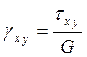
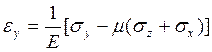
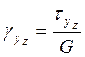
                (I)                        (II)

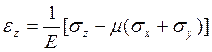
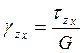
Для изотропного тела главные оси напряженного и деформированного состояний совпадают.  Это непосредственно следует из соотношений (II).

В частности:

 ;                ;           ;              ;            

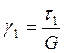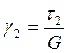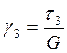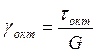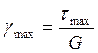
Но   

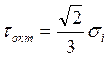
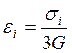                          или       

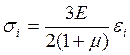
5. Условия возникновения пластических деформаций (условия пластичности).

При одноосном растяжении вопрос решается просто:

(;  )

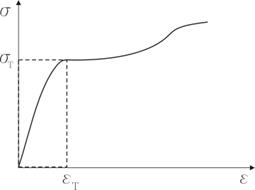
Условие пластичности     

При сложном напряженном состоянии:

         1) Условие пластичности наибольших касательных напряжений (Треска-Сен-Венана).

Пластические деформации наступают тогда, когда наибольшее касательное напряжение  достигает некоторого определенного для  данного материала значения   независимо от вида напряженного состояния, т.е.