Основы деформационной теории пластичности (теория малых упругопластических деформаций), страница 2

Для одноосного напряженного состояния :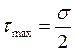  

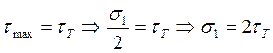Условие пластичности:    или  ,  но   

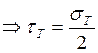
Для сложного напряженного состояния:

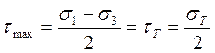
         2) Условие пластичности удельной энергии формоизменения (условие Хубера-Мизеса).

Пластическое состояние наступает тогда, когда удельная энергия формоизменения достигает некоторого предельного значения.

Математически  это условие можно свести к записи:

или

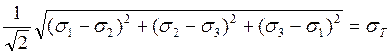, т.е. пластические деформации возникают тогда, когда интенсивность напряжений достигает величины предела текучести материала при растяжении.

Для одноосного напряженного состояния отсюда следует:

4. Зависимость между напряжением и деформацией за пределами упругости

при одноосном напряженном состоянии.

             

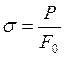
Зависимость между напряжением и деформацией при одноосном напряженном состоянии дается диаграммой растяжения, которую получают при экспериментальном исследовании.

В упругой стадии:     

В пластической стадии: ,    где 

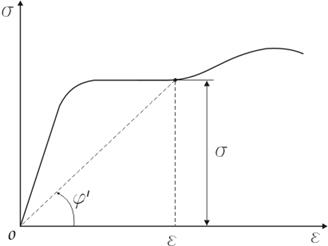
Ограничимся рассмотрением малых упруго-пластических деформаций:

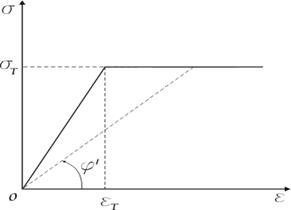
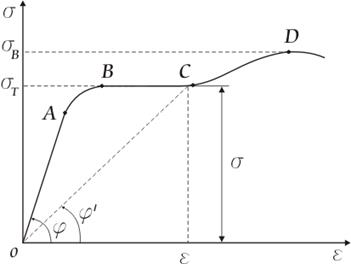
Схематизированная диаграмма растяжения (диаграмма растяжения идеального упруго-пластического тела).

6. Основные гипотезы деформационной теории пластичности

(теории малых упруго-пластических деформаций).

Основными гипотезами, на основе которых устанавливаются зависимости между напряжениями и деформациями за пределами упругости (справедливые и в пределах упругости) по теории малых упруго-пластических деформаций, является следующие:

         1)   Гипотеза о неизменности объема элемента

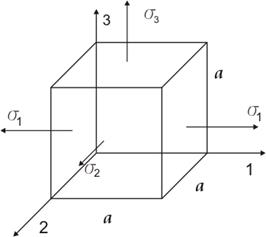
главные линейные деформации

     

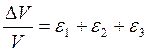                                                                           (1)

- относительное изменение объема, независимо от того,  в какой стадии работает материал.

Пусть материал работает в пределах упругости. Тогда, применяя обобщенный закон Гука, получим:

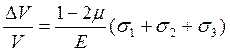                                                                  (2)

По аналогии с выражением (2) и для пластического состояния формально можно записать:

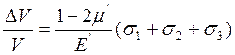                                                                   (3)

Но в пластической области величины ,   –  и зависят от степени деформирования.

Эксперимент показывает, что обычно изменение объема в пластической стадии следует упругому закону, т.е. величина

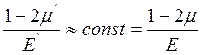, т.е. изменение объема невелико, хотя величина деформаций значительна.

Учитывая это, при решении инженерных задач за пределами упругости полагают, что изменением объема можно пренебречь. Тогда на основании соотношения (1) можно положить

                                                                        (4)

В этом случае принято говорить, что материал несжимаем, а условие (4) представляет собой условие несжимаемости.

В соответствии с соотношением (3) гипотезе о неизменности объема эквивалентно допущение, что в пластической стадии

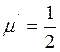                                                                                (5)

Эксперимент подтверждает, что действительно  при увеличении пластических деформаций.

         2) Направления главных осей напряженного и деформированного состояния совпадают и за пределами упругости, а главные касательные напряжения пропорциональны главным угловым деформациям.

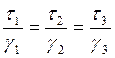
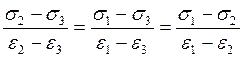                                                        (6)

         3) Интенсивность напряжений является и для каждого материала вполне определенной и не зависящей от вида напряженного состояния функцией интенсивности деформацией.

                                                                              (7)

7. Основные соотношения деформационной теории пластичности.

Определим вид функции   в соотношении (7).

Для этого рассмотрим случай простого растяжения.

,   ()

Для простого растяжения:         ,    

,      

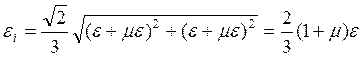
В пластической области 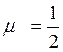  согласно (5)        

Таким образом, для простого растяжения функция  определяется диаграммой растяжения, т.е.

Но по III гипотезе эта функция не зависит от вида напряженного состояния, т.е. для любого напряженного состояния:

, где  берется по диаграмме растяжения, т.е. диаграмма деформирования (график зависимости ) совпадает с диаграммой растяжения.

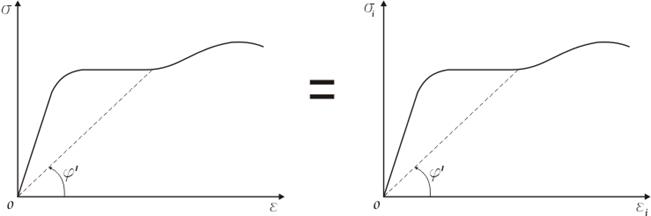
Установим зависимость между напряжениями и деформациями за пределами упругости.

Распишем соотношение (8).

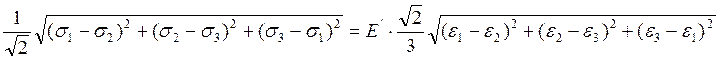        -  (9)

Разделим соотношение (9) на () и преобразуем:

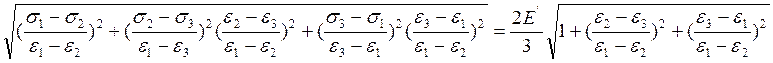
-  (10)

Но из соотношений (6) следует:

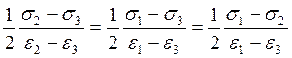                                                                      -  (11)