Следовательно, из (10) получаем
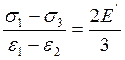 (12)
(12)
или
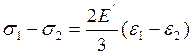 (13)
(13)
Аналогично, воспользовавшись (11), получим
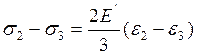 (14)
(14)
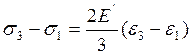 (15)
(15)
Кроме того, из (12) и (11) имеем:
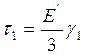
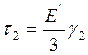 (16)
(16)
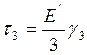
Умножим соотношение (14) на 2, соотношение (15) на 3 и сложим с соотношением (13):
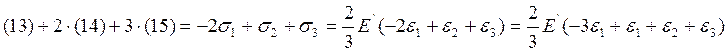
Но ![]() (условие несжимаемости
материала)
(условие несжимаемости
материала)
Следовательно,
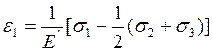 (17)
(17)
Аналогично, меняя порядок сомножителей, получим:
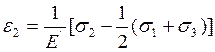 (18)
(18)
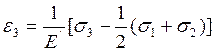 (19)
(19)
Соотношения (17) - (19) и (16) являются основными в теории малых упруго-пластических деформаций.
При использовании этих
формул следует помнить, что ![]() зависит от степени
деформирования и является переменной величиной.
зависит от степени
деформирования и является переменной величиной.
Величина ![]() определяется из диаграммы деформирования
определяется из диаграммы деформирования ![]() , если известно значение
, если известно значение ![]() или
или![]() .
.
Например, в случае диаграммы Прандтля
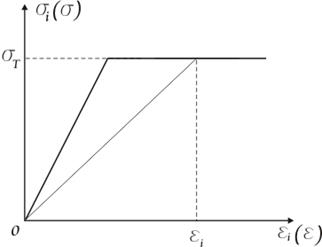
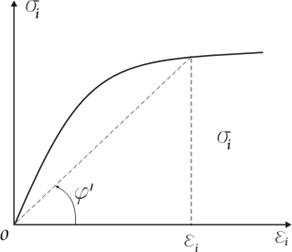
![]()
НЕСУЩАЯ СПОСОБНОСТЬ ТОЛСТОСТЕННОГО ЦИЛИНДРА
ПОД ВНУТРЕННИМ ДАВЛЕНИЕМ
1. Цилиндр длинный, участки, примыкающие к днищам, исключаем из рассмотрения.
2. Материал цилиндра идеальный упруго-пластический;
3. Критерий пластичности Треска-Сен-Венана.
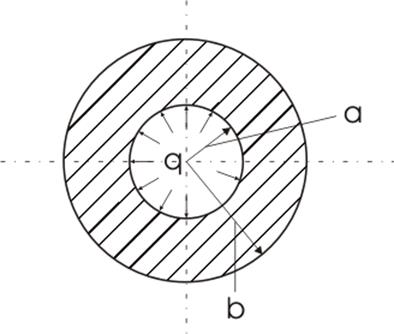
Решение задачи Ламе (работа цилиндра в упругой стадии):
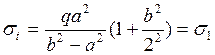
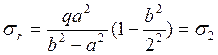
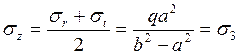
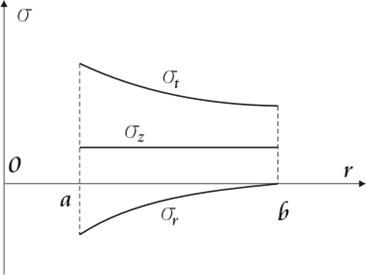
Начало пластических деформаций
(конец упругой стадии работы) – необходимо выполнить условие при ![]() :
: ![]()
(по критериям Треска-Сен-Венана), т.е.
![]()
![]()
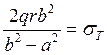
откуда
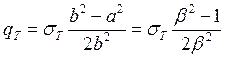 , (
, (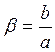 - коэффициент толстостенности)
- коэффициент толстостенности)
Итак, в толстостенном цилиндре пластические деформации возникают на внутренней поверхности, но они не могут свободно развиваться, т.к. внутренний слой окружен материалом, работающим в упругой стадии.
Пластические деформации, которые не могут свободно развиваться, называются стесненными.
При увеличении давления, пластические деформации охватывают некоторый слой материала, но продолжают оставаться стесненными.
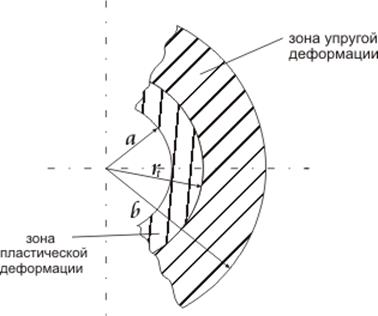
Свободное развитие пластических деформаций начнется тогда, когда пластическая зона (фронт пластической деформации) достигнет наружной поверхности (упругий слой исчезнет). Такое состояние цилиндра называется предельным состоянием.
Давление, при котором начинают развиваться
нестесненные пластические деформации, называют несущей способностью цилиндра
и обозначают ![]() .
.
![]()
Рассмотрим равновесие элемента цилиндра в предельном состоянии.
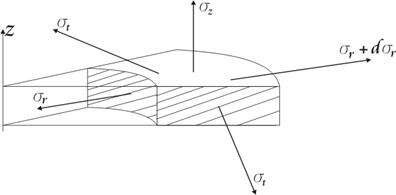
Уравнения равновесия не
зависят от физических свойств материала, поэтому уравнение равновесия в
проекциях на направление ![]() , полученное ранее,
остается в силе:
, полученное ранее,
остается в силе:
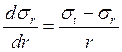
Применяя условие пластичности Треска Сен-Венана, имеем:
![]()
Таким образом,
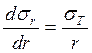
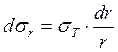
![]()
![]()
при ![]() :
: ![]()
![]()
![]()
![]()
![]()
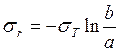
Весь материал цилиндра находится в пластическом состоянии. Из условия пластичности Треска Сен-Венана следует:
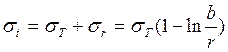
при ![]() :
: ![]()
![]()
![]()
При ![]()

![]()
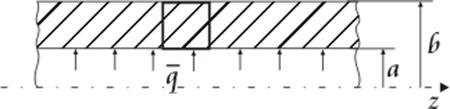
Сечения цилиндра (поперечные) остаются плоскими. Следовательно,
![]() (1)
(1)
(геометрическое условие).
В пластической области
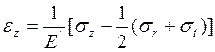 (2)
(2)
Условие равновесия отсеченной части для цилиндра с днищами
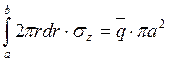 (3)
(3)
(условие статики)
Выражая ![]() из (2), получим
из (2), получим
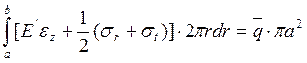 (4)
(4)
Из условия равновесия элемента
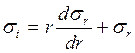 (5)
(5)
Подставляя в (4), получим
![]()
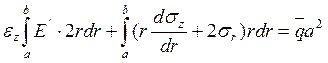 (6)
(6)
![]()
![]()
![]()
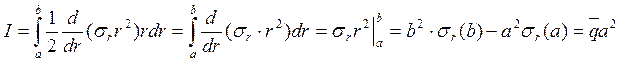
![]()
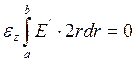 (7)
(7)
![]()
![]() (8)
(8)
Тогда из (2), учитывая (8), получим 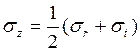 (9)
(9)
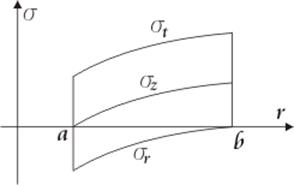
Исследование напряженного состояния цилиндра
в упруго-пластической области
Рассматривается случай ![]() .
.
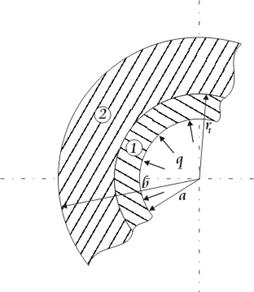
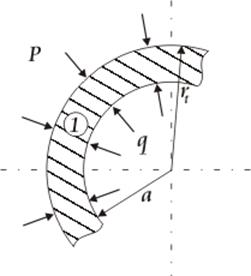
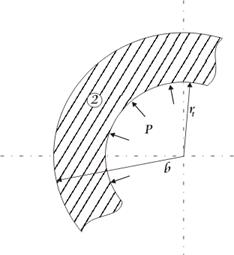
Для зоны 2:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.