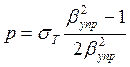Основы деформационной теории пластичности (теория малых упругопластических деформаций), страница 4

                                                                      (10)                  

()

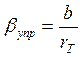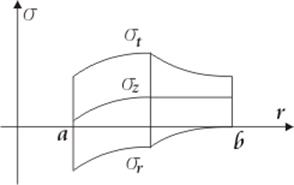
Для зоны 1:

                                                                 (11)

Граничные условия:                         

                 

Подставляя граничные условия в (11), имеем:

 

                 

 

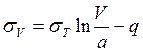
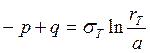                                                                                                                             (12);                        

                                          

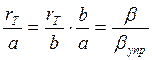
                                                                                                                                                                                         (13)

Подставляя выражение (10) для P, имеем:

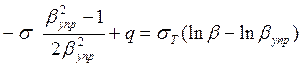                                           (14)         

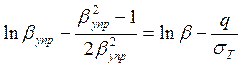                                                                                                          (15)

Из уравнения (15) определим      ()

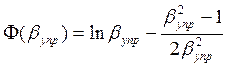
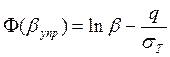                                                        (16)

;

;

;

;

;

;

()

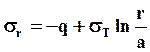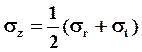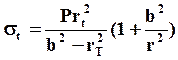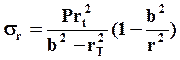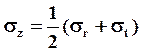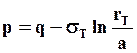При      

В этом случае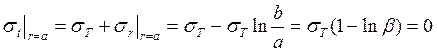    

Решение задачи о несущей способности толстостенного цилиндра

при использовании условия пластичности Хубера-Мизеса

Уравнение равновесия остается прежним

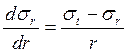
Критерий пластичности  Хубера-Мизеса

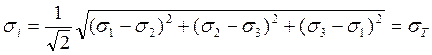
учитывает влияние   в отличие от условия Треска-Сен-Венана.

Для цилиндра:  

           

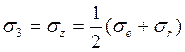
- следует из гипотезы о неизменности   объема.

Таким образом,

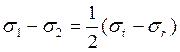
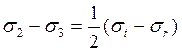
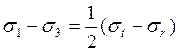
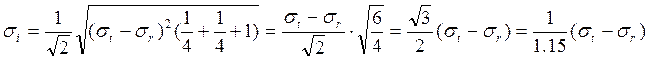
Условие пластичности принимает вид:

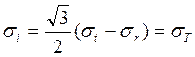
Следовательно, предельное давление по критерию Хубера-Мизеса:

Оценка степени деформирования цилиндра в предельном состоянии

Для сложного напряженно-деформированного состояния

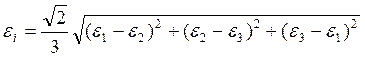
Условие несжимаемости материала цилиндра:

Кроме того, мы получили ранее:

Поэтому,

;           ;      

;     

;         

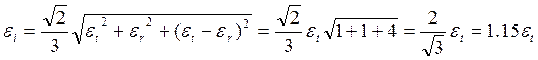
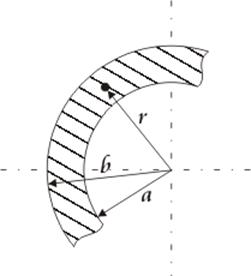
Определим соотношение  .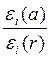

    

  

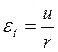
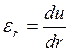
Но                                    

        

;                            

;                     

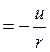
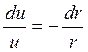
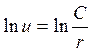
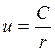
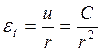
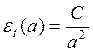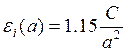
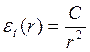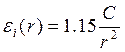
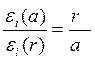
В частности,  при  :

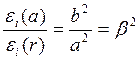
Но        - конец упругой стадии             при        

Эксперимент показывает, что величина деформаций    практически не влияет на коррозионную стойкость материала.

.

Нормы и методы расчета на прочность сосудов и аппаратов,

работающих под давлением  (ГОСТ 14249-89)

В своей работе конструктор использует для расчета проектируемых объектов нормы, которые могут отраслевыми, общероссийскими, либо возведенными в ранг государственного стандарта.

ГОСТ 14249-89 регламентирует нормы и методы расчета на прочность сосудов и аппаратов.

Рассмотрим расчетные формулы, приведенные в стандарте, для расчета сосудов цилиндрической формы, работающих под давлением с точки зрения полученных нами результатов при исследовании толстостенного цилиндра.

Принимая в качестве условия пластичности условие Треска-Сен-Венана, мы получим

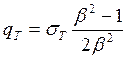
Интервал между этими значениями давления зависит от толстостенности цилиндра:

Рабочее давление назначается как часть предельного давления посредством введения коэффициента запаса прочности  .  По нормам  .

Если в качестве предельного принять давление 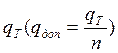  , то получим расчет по допускаемым напряжениям, т.к. это означает, что мы допускаем в наиболее опасной точке напряжение .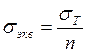

Целесообразно в качестве предельного  принять давление  . В этом случае:

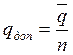
Имеем запас  по давлению.

Рассмотрим подробнее формулу:

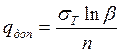
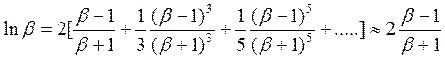
При   посредством этой формулы    в сторону запаса прочности

(      )

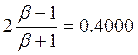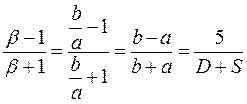
S - толщина стенки                         

D - внутренний диаметр цилиндра

-   

Следовательно,

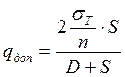
Из этой формулы легко можно получить формулу для исполнительной толщины цилиндра по заданному давлению :

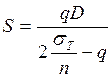
В ГОСТ 14249-73 эти формулы имеют следующий вид:

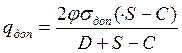
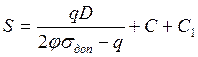
- условно допускаемое напряжение

 -  коэффициент, характеризующий прочность сварного шва в сравнении с                                                                                      прочностью основного металла

C - прибавка к расчетной толщине на коррозию

 - технологическая прибавка