Исходные данные.
![]()
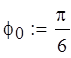
![]()
![]()
![]()
![]()
![]()
![]()
1. Безмоментное решение.
Сфера.
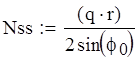
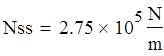
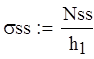
![]()
![]()
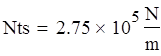
![]()
![]()
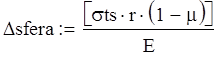
![]()
Цилиндр.
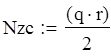
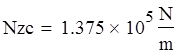
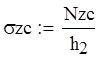
![]()
![]()
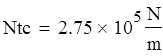
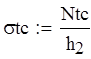
![]()
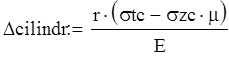
![]()
Вывод: по безмоментной теории перемещения цилиндра и сферы в месте стыка не равны, что соответствует нарушению сплошности, поэтому необходимо применить более точную теорию расчета стыка поверхностей.
2. Моментное решение.
Воспользуемся методом сечений: рассечем аппарат в сечении стыковки цилиндрической обечайки и сферического днища, "отбросим" одну часть от другой, заменим действие частей друг на друга усилиями и определим эти усилия из условия целостности (cплошности) аппарата.
![]()
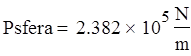
Сфера:
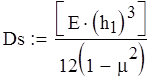
![]()
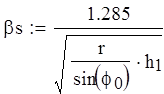
![]()
Цилиндр:
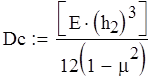
![]()
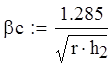
![]()
Из условия равенства линейных и угловых перемещений найдем значения M и P:
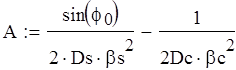
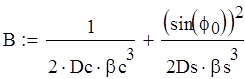
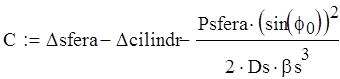
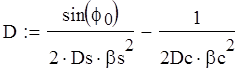
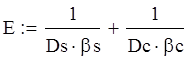

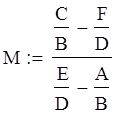
![]()
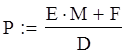
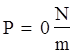
Сопоставляем результаты расчета с решением для абсолютно жесткого днища:
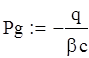
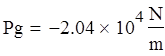
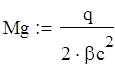
![]()
Для нахождения опасного сечения строим эпюры
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
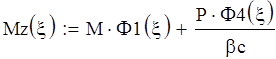
![]()
![]()
Эпюры силовых факторов:

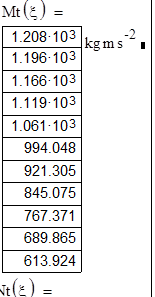
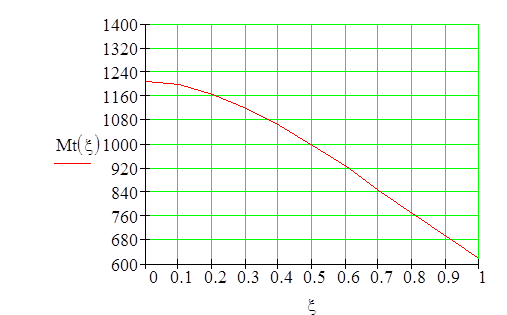

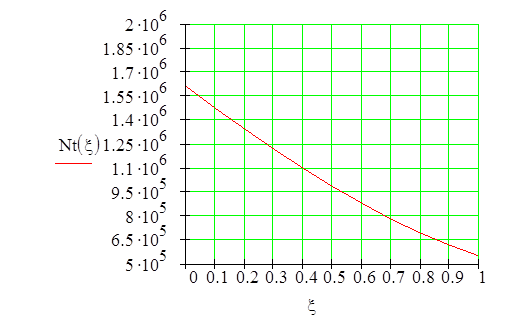
Опасным сечением является то, где Mz=max
![]()
![]()
Вывод: опасное сечение x=0.
Вычисляем напряжения в опасном сечении:
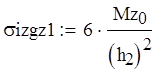
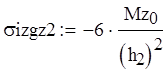
![]()
![]()
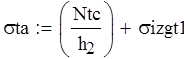
![]()
![]()
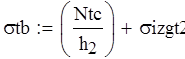
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Вычисляем эквивалентное напряжение используя третью и четвертую теории прочности:
3 теория прочности:
![]()
![]()
![]()
![]()
![]()
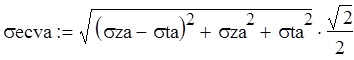
![]()
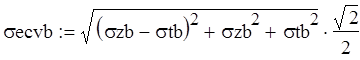
![]()
За опасную точку выбираем ту, где
![]()
=max
Вывод: опасное сечение А
Эквивалентное напряжение в опасном сечении следует сопоставить с пределом текучести материала и выбрать материал таким образом, чтобы запас прочности превышал единицу: Ст3
![]()
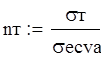
![]()
Расчет эквивалентной нагрузки:
![]()
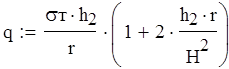
![]()
Жестко заделаная оболочка:
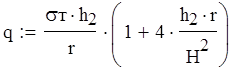
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.