Измерение линейных перемещений с помощью индуктивных датчиков: Методические указания к выполнению лабораторной работы, страница 2

Из выражения (1.6) видно, что тяговое усилие является нелинейной функцией входного перемещения и при постоянных значениях остальных величин обратно пропорционально частоте тока.

Для компенсации тягового усилия якорь датчика часто укрепляют на пластинчатой пружине с жёсткостью:

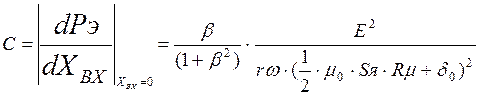                                     (1.7)

Однако вследствие нелинейности тяговой характеристики полная компенсация тягового усилия возможна лишь при . Большое входное усилие является недостатком однотактного датчика. Другой недостаток состоит в том, что статическая характеристика датчика не начинается от нуля.

Эти недостатки значительно меньше у двухтактного датчика. включенного по дифференциальной схеме (рисунок 3). Дифференциальная схема включения любого двухтактного датчика в общем случае является мостовой схемой с той лишь разницей, что нагрузка имеет среднюю точку, соединенную с источником тока. выходное напряжение измеряется между крайними клеммами нагрузки. Нагрузкой со средней точкой являются, например, входы двухтактного электронного усилителя, электродвигателя и электромашинного усилителя с двумя обмотками возбуждения.

Если поменять местами клеммы Е и U_вых, то нагрузка будет включена без средней точки, а сопротивления r_Н, станут балластными.

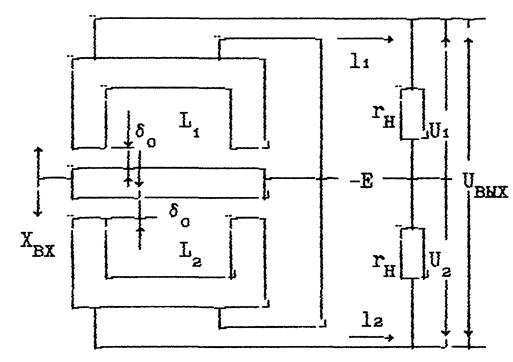
Рисунок 3 – Дифференциальная схема двухтактного датчика

Такая схема называется мостовой. Мостовые схемы менее экономичны, чем дифференциальные, из-за потери мощности в балластных сопротивлениях и применяются для маломощных датчиков, например емкостных.

Двухтактный датчик, включенный по дифференциальной схеме, имеет две независимые идентичные электрические цепи. Выходное напряжение равно разности напряжений на двух половинах сопротивления нагрузки U_вых=U₁-U₂. Входное перемещение Х_вх отсчитывается от среднего положения якоря между двумя ярмами например, положительное – вниз. Отрицательное – вверх, на якорь действует сила, равная разности сил притяжения его со стороны каждого ярма. Эта сила равна нулю при Х_вх=0. Для значений Х_вх, близких к нулю, силу, действующую на якорь, можно скомпенсировать установкой якоря на пружине с определенной жесткостью.

Характеристика двухтактного датчика геометрически (с учетом сдвига фаз) складывается из характеристик обоих составляющих его однотактных датчиков (рисунок 3). Характеристика U₂=U₂(X_вх) является зеркальным отражением характеристики U₁=U₁(X_вх) относительно оси ординат вследствие симметрии схемы. Кривая – U₂(X_вх) – зеркальное отражение характеристики U₂(X_вх) относительно оси абсцисс. Сложив алгебраические ординаты кривых U₁(X_вх) и U₂(X_вх) получим приближённую (без учёта сдвига угла сдвига фаз ) статическую характеристику UВЫХ=UВЫХ(XВХ) двухтактного датчика. Из кривых на рисунке 3 видно, что результирующая характеристика двухтактного датчика более линейна, чем характеристика датчиков его составляющих.

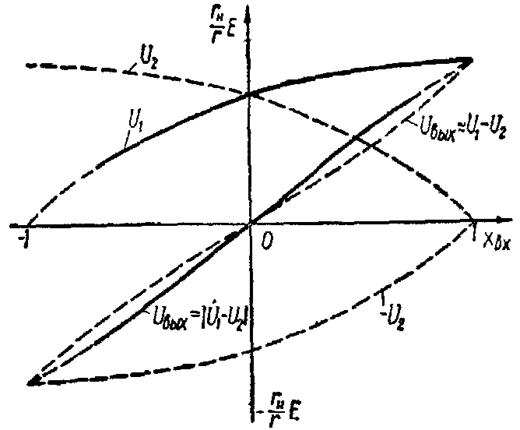
Рисунок 4 – Построение статической характеристики двухтактного индуктивного датчика при β = 1

Двухтактный датчик имеет наибольшую чувствительность в области значений Х_вх, близких к нулю. При переходе значения входного перемещения через нуль фаза напряжения на выходе изменяется на 180°, что соответствует на статической характеристике условному изменению знака действующего напряжения U_вых.

Рассмотрим аналитическое выражение статической характеристики двухтактного индукционного датчика. Если для первого такта выходное напряжение определяется уравнением (1.2), то для второго, в этом уравнении нужно изменить знаки перед ,тогда получим:

                   

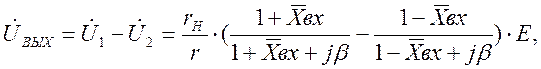
или

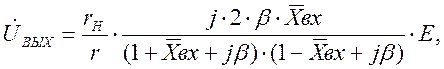                                           (1.8)

откуда модуль U_вых

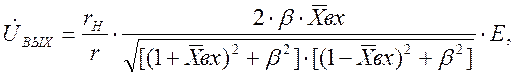                               (1.9)

Из выражения (1.9) видно, что зависимость U_вых от _вх нелинейная. Чем меньше β т.е. чем меньше индуктивное сопротивление wL по сравнению с активным r, тем сильнее отличается статическая характеристика двухтактного датчика от прямой линии.

При расчётах систем автоматического регулирования целесообразно знать величину чувствительности двухтактного датчика в области близкой к _вх= 0. Из выражения (1.9) можно получить выражение для относительной чувствительности датчика:

                          

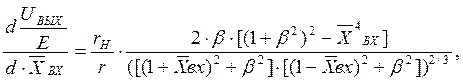
При _вх=0

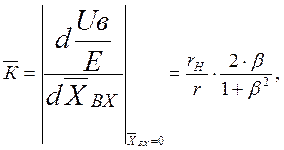                                                                   (1.10)

Приравняв  нулю, найдём оптимальное значение β, при котором относительная чувствительность максимальна. Когда активное сопротивление цепи одного датчика равно его индуктивному сопротивлению при _вх=0 β_опт=1. При этом получаем

                                                      

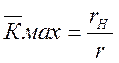
или

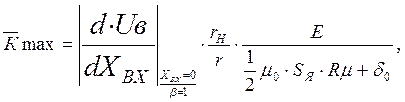                                               (1.11)

Результирующее тяговое усилие согласно уравнению (1.6)

    

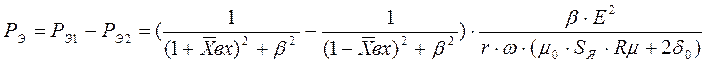
После преобразования получаем:

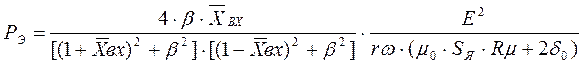                (1.12)

Из этого выражения легко определить значение жесткости компенсирующей пружины

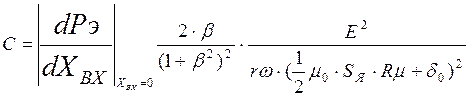                                     (1.13)