Измерение линейных перемещений с помощью индуктивных датчиков: Методические указания к выполнению лабораторной работы, страница 3

Из выражения (1.12) и (1.13) видно, что жесткость компенсирующей пружины для двухтактного датчика больше в два раза по сравнению с однотактным. Зависимость тягового усилия от _вх, определяемая уравнением (1.12), более линейная, чем уравнением (1.6). Поэтому пружина компенсирует тяговое усилие в двухтактном датчике при больших значениях |Xвх|, чем в однотактном. Пружину можно не устанавливать, если элемент, к выходу которого присоединён индуктивный датчик, обладает упругостью. Тогда при расчете этого элемента его жесткость следует увеличить на величину С, определяемую уравнением (1.13).

Двухтактный датчик можно включить по мостовой схеме (рисунок 4). Тогда внутреннее сопротивление схемы

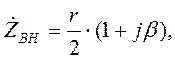                                                                                      (1.14)

где β=ωL₀/r; r=r_б+r_обм;

r_б – балластное сопротивление.

Напряжение на выходе в режиме холостого хода

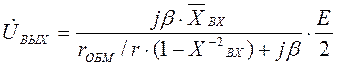                                                           (1.15)

При β=1 и r_обм < r

                                   

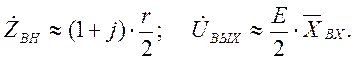
В этом случае статическая характеристика датчика в режиме холостого хода (Zн=∞) практически линейна, так как Z_вн не зависит от Х_вх, то нагрузочные характеристики линейны, но более пологие, чем характеристика холостого хода.

Мостовая схема по сравнению с дифференциальной имеет примерно в 2.8 раза меньшую относительную чувствительность при согласованной нагрузке.

Абсолютная чувствительность двухтактных датчиков с плоскопараллельным воздушным зазором может превышать 300 В/мм. Порог чувствительности некоторых датчиков при тщательной экранировке и балансировке схемы в нейтральном положении якоря составляет сотые доли микрона.

Легко сконструировать датчики с выходной мощностью порядка десятков ватт. Габариты и вес датчика увеличиваются с увеличением выходной мощности и уменьшаются с увеличением частоты тока.

Как видно из формул (1.6) и (1.13), с увеличением частоты входное усилие уменьшается. Однако на очень большой частоте начинают влиять межвитковые емкости, вследствие чего затрудняется балансировка датчика в нейтральное положение якоря, т.е. уравновешивание моста по активным и реактивным составляющим.

         

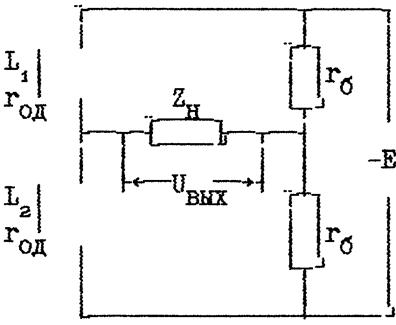
Рисунок 5 – Мостовая схема двухтактного индуктивного датчика

Разновидностью дифференциального индуктивного преобразователя является плунжерный преобразователь (рисунок 6). Конструктивное отличие его - применение металлического стального плунжера 1. перемещающегося внутри цилиндрических катушек 2 и 3, вместо плоского якоря, позволяет получать значительно больший диапазон величин измеряемых перемещений. Способ включения катушек 2 и 3 в измерительную схему остается тем же. При среднем (нулевом положении плунжера ток I_пр через измерительный прибор-указатель (R_пр) равен нулю. В случае смещения плунжера от среднего положения через прибор начнет протекать ток, по величине пропорциональной величине смещения плунжера и по направлению соответствующий направлению смещения. На рисунке 7 даны также характеристики плунжерного датчика (практически линейные)

                                    I_пр=f₁(δ%);   Х₁=f₂(δ%);   Х₂=f₃(δ%),

где Х₁, Х₂ - реактивные сопротивления катушек с учетом их взаимной индуктивности. В плунжерном преобразователе влияние рассеяния магнитного потока более заметно и его необходимо учитывать.

Все рассмотренные здесь преобразователи основаны на изменении индуктивности катушек при перемещениях якоря. Преобразователи, основанные на принципе изменения взаимной индуктивности катушек при перемещении якоря, т.е. трансформаторные индуктивные преобразователи, также широко применяются.

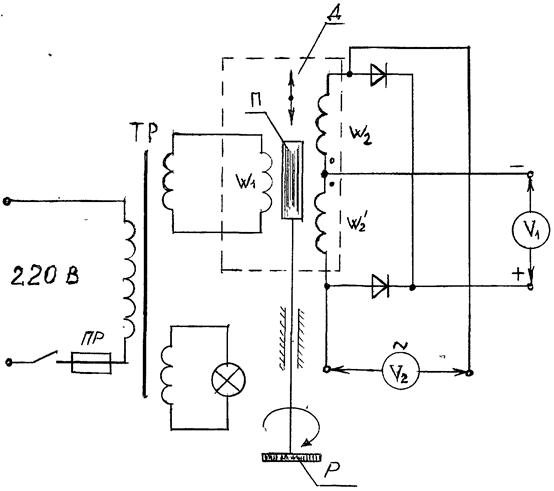
Рисунок 6 – Принципиальная электрическая схема дифференциального плунжерно-индуктивного датчика

ТР – питающий трансформатор;

Д – датчик дифференциальный плунжерный;

W1 – питающая обмотка датчика;

W₂^/, W₂ – вторичные обмотки датчика включенные встречно;

V₁ – вольтметр постоянного тока;

V₂ – вольтметр переменного тока;

Р – ручка изменения положения плунжера;

П – плунжер;

ПР – плавкая вставка.

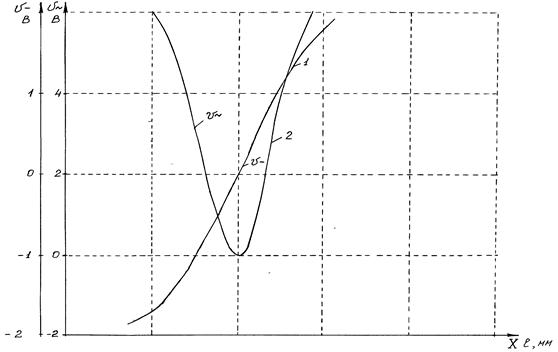
Рисунок 7 – Статическая характеристика датчика

1 – кривая выходного напряжения датчика по постоянному току;

2 – кривая выходного напряжения датчика по переменному току.

3 Порядок выполнения работы

3.1 Подучить допуск к лабораторной работе, представив для этого подготовленный материал (п.п 1.2 – 1.4 раздела "Самостоятельная подготовка").

3.2 Исследовать простую схему индуктивного датчика, для которого магнитное сопротивление определяется по формуле, пренебрегая магнитным сопротивлением участка цепи со сталью, т.к. оно мало по сравнению с сопротивлением зазора:

                                                  R_м=R_в=2δ/(μ₀ S_в),

где Rв - сопротивление участка с воздушным зазором;

δ – величина воздушного зазора между статором и якорем;

μ₀ – магнитная проницаемость воздуха;

S_в – площадь поперечного сечения стали в воздушном зазоре.

Необходимо помнить, что величина этого сопротивления и параметров катушки зависит от индуктивности датчика, которая в свою очередь зависит от частоты питающего напряжения сети:

                                                xl =  ω [W²/2δ] μ₀ S_в,

где W – число витков катушки датчика;

ω = 2πf – круговая частота питающей сети;