Методические указания к лабораторным работам по курсу “Информатика” (пакет MathCAD, часть 2)

ЛАБОРАТОРНАЯ РАБОТА 5

ЛИНЕЙНАЯ И СПЛАЙН-ИНТЕРПОЛЯЦИЯ И ЭКСТРАПОЛЯЦИЯ

Интерполяция – нахождение промежуточных величин числовой последовательности по некоторым известным ее значениям в узловых точках.

Экстраполяция - нахождение выходящих за пределы конечных точек числовой последовательности значений.

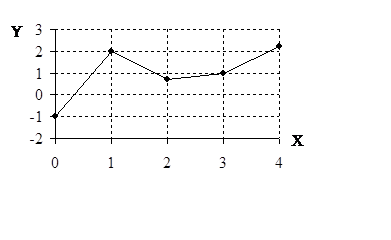В технике широко используется зависимости вида y = f(x), задаваемые значениями X и Y в узловых точках:

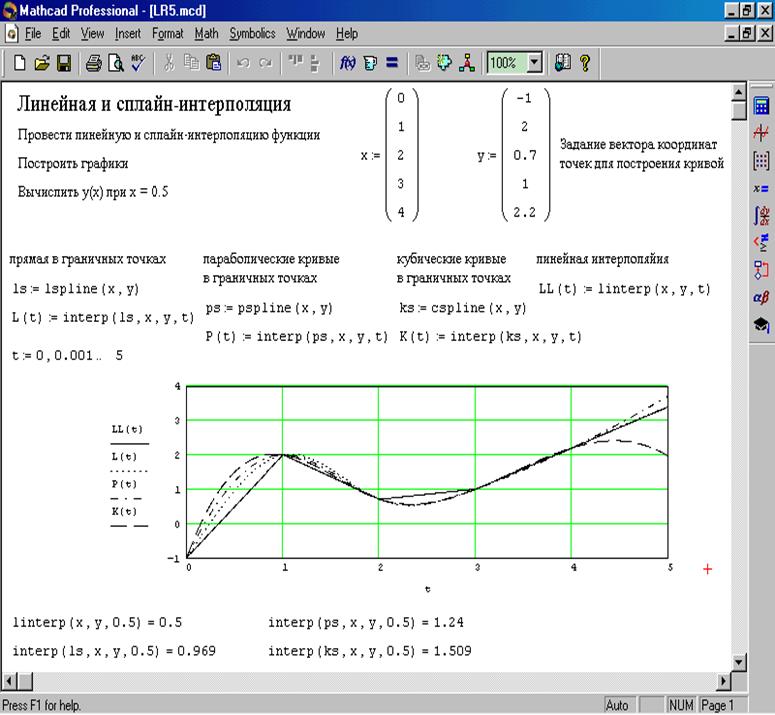
При линейной интерполяции узловые точки соединяются отрезками прямых. Линейная интерполяция реализуется с помощью функции: linterp(x,y,xt) определяющей значение y(x) для заданного x. Здесь x и y - векторы x и y, xt - текущее значение x, для которого необходим расчет y(x). Линейная интерполяция используется для гладких функций с большим числом узлов интерполяции.

При сплайн-интерполяции зависимость y(x) заменяется кусками полиномов третьей степени. Сплайн-интерполяция реализуется с помощью функции: interp(vs,x,y,xt). Функция определяет интерполируемое значение y, соответствующее аргументу xt. vs - это вектор коэффициентов вторых производных, вычисляемый на основе векторов x и y одной из функций:

lspline(x,y)– генерирует кривую сплайна, которая приближается к прямой линии в граничных точках;

pspline(x,y)– генерирует кривую сплайна, которая приближается к параболе в граничных точках;

cspline(x,y)– генерирует кривую сплайна, которая приближается к кубическому полиному в граничных точках.

Эти функции возвращают вектор коэффициентов вторых производных. Аргументы x и y должны быть вещественными векторами одинаковой длины. Значения x должны быть расположены по возрастанию.

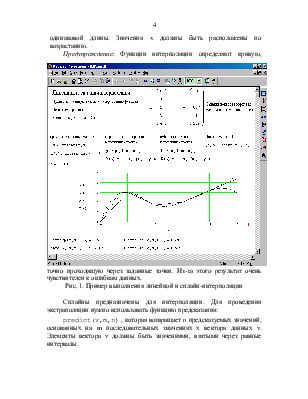
Предупреждение: Функции интерполяции определяют кривую, точно проходящую через заданные точки. Из-за этого результат очень чувствителен к ошибкам данных. 

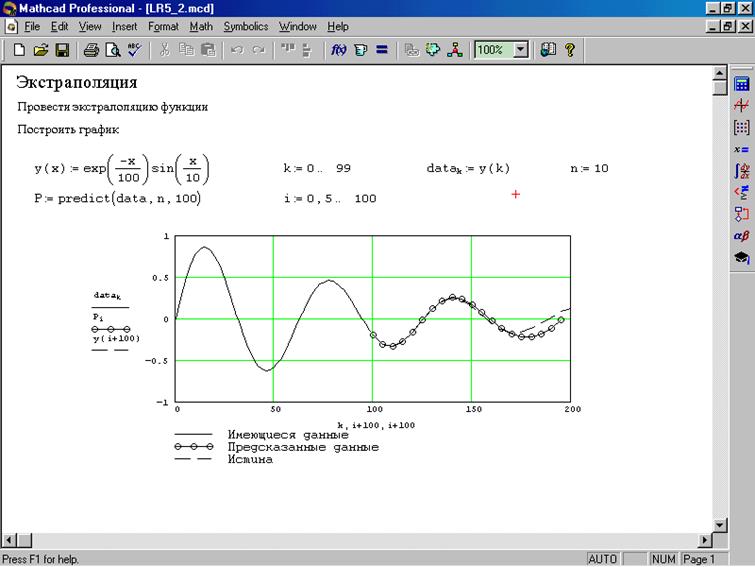
Сплайны предназначены для интерполяции. Для проведения экстраполяции нужно использовать функцию предсказания:

predict(v,m,n) , которая возвращает n предсказуемых значений, основанных на m последовательных значениях х вектора данных v. Элементы вектора v должны быть значениями, взятыми через равные интервалы.

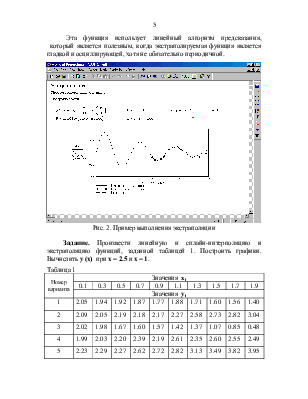
Эта функция использует линейный алгоритм предсказания, который является полезным, когда экстраполируемая функция является гладкой и осциллирующей, хотя не обязательно периодичной.

Задание. Произвести линейную и сплайн-интерполяцию и экстраполяцию функций, заданной таблицей 1. Построить графики. Вычислить у (х)  при х = 2.5 и х = 1.

Таблица 1