Информатика и выч. техника \ Информатика

Методические указания к лабораторным работам по курсу “Информатика” (пакет MathCAD, часть 2), страница 3

slope(x,y)-определяет наклон линии регрессии (коэффициент b).

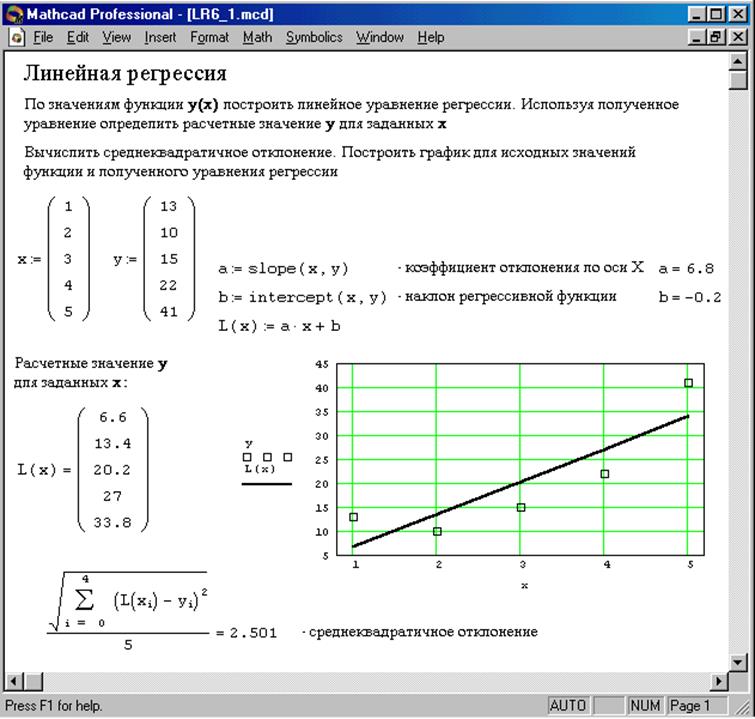
Рис. 3. Линейная регресия

Квадратичная регрессия – определение коэффициентов квадратичного уравнения f(x) = a0 + a1·x + a2·x2, для набора данных φ(x).

linfit(x,y,F) - определяет коэффициенты регрессионного  уравнения по шаблону F;

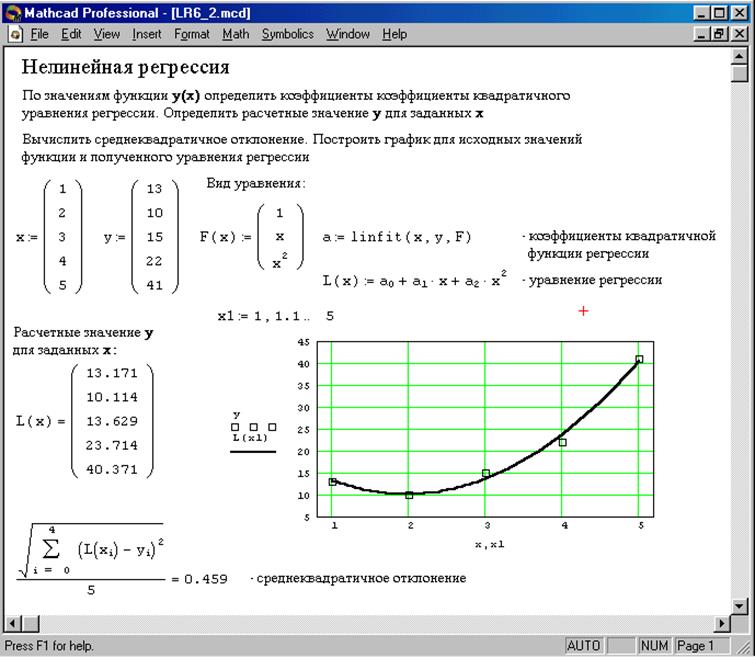
Рис.4. Нелинейная регрессия

Задание 1.

1)  По значениям функции, заданной в таблице 1, построить линейное уравнение регрессии.

2)  Используя полученное уравнение, определить расчетное значение y для всех значений x, приведенных в таблице 1.

3)  Вычислить среднеквадратичное отклонение.

4)  В одной системе координат построить графики по значениям функции, заданным в таблице 1.

Задание 2.

1)  По значениям функции, заданной в таблице 1, определить коэффициенты квадратичного регрессионного уравнения.

2)  Используя полученное уравнение, определить расчетное значение y для всех значений x, приведенных в таблице 1.

3)  Вычислить среднеквадратичное отклонение и сравнить со значением, полученным для линейного уравнения регрессии.

4)  График, построенный в пункте 4 задания 1 достроить квадратичным регрессионным уравнением.

Контрольные вопросы:

1)  Что такое уравнение регрессии.

2)  Записать и разъяснить уравнения линейной и квадратичной регрессии.

3)  Как определяется погрешность уравнения регрессии.

ЛАБОРАТОРНАЯ РАБОТА  7

ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ПЕРВОГО ПОРЯДКА

Дифференциальное уравнение – уравнение, содержащие неизвестную функцию одного или нескольких переменных, независимые переменные и производные неизвестной функции по независимым переменным.

Решение дифференциального уравнения – нахождение всех известных функций, обращающих уравнение в тождество.

Рассмотрим решение простого дифференциального уравнения.

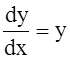, или y' = f (x, y).                                         (1)

Решением этого уравнения является тождество:

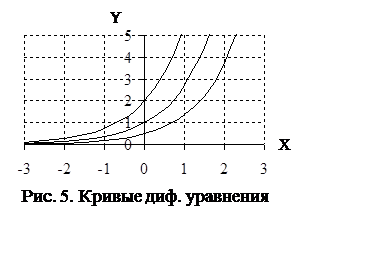
,                                                     (2)

где С – произвольная постоянная. При различных значениях постоянной С получается семейство кривых удовлетворяющих исходному дифференциальному уравнению. На рисунке 5 представлено решение дифференциального уравнения для постоянной С равной 2, 1 и 0.5. Для получения конкретного решения задается начальное условие

у(х0) = у0 ,                                                     (3)

например, при х = 0, у = 1, т.е. у(0) = 1. Из уравнения (2) получаем: ; С = 1, тогда решением является кривая .

Задача о нахождении частного решения дифференциального уравнения (1), при начальном условии (3)  получила название задача Коши.

Существует множество классических способов решения дифференциальных уравнений. Однако в большинстве практических задач классические методы либо вообще не приемлемы, либо приводят к сложным и трудоемким решениям. В таких случаях используют численные методы.

Задача численного интегрирования состоит в построении таблицы значений функции у(х) в точках х1 , х2 , … хn  по заданному дифференциальному уравнению и начальному условию.

Существует ряд способов численного решения задачи Коши (численного интегрирования).

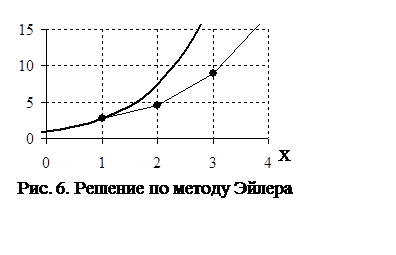Метод Эйлера заключается в следующем: согласно задачи Коши в любой точке с координатами (х, у) по заданному дифференциальному уравнению можно вычислить производную, которая является наклоном касательной к искомой кривой (геометрический смысл производной).  Используя это условие, одношаговым методом, определяется наклон касательной в начальной точке х1 , далее продвинувшись на шаг h вдоль полученной касательной до следующей точки вновь определяется наклон касательной, и т.д. (рис. 6). Координаты каждой последующей точки определяются следующим образом:

хi+1 = хi + h;                                                    (4)

yi+1 = yi + h · f(xi, yi);                                     (5)

Недостаток метода Эйлера состоит в накапливающейся с каждым шагом погрешности вычислений, которая зависит от величины шага. Метод дает приемлемые результаты только при очень малом шаге, увеличивающем затраты времени на решение.

Метод Рунге-Кутта также является одношаговым методом, но позволяет с большей точностью решать задачу Коши. Это достигается за счет уточнения среднего значения касательной к функции по четырем специально подобранным точкам для каждого шага.

Скачать файл