Методические указания к лабораторным работам по курсу “Информатика” (пакет MathCAD, часть 2), страница 5

Контрольные вопросы:

1)  Чем определяется погрешность численного решения системы дифференциальных уравнений методом Эйлера.

ЛАБОРАТОРНАЯ РАБОТА  9

РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ II^-ГО ПОРЯДКА

Одним из способов решения дифференциальных уравнений n-го порядка является способ понижения степени дифференциального уравнения т.е. приведение к системе дифференциальных уравнений первого порядка.

Пусть задано дифференциальное уравнение второго порядка:

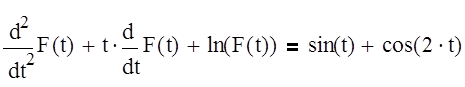,  (6)

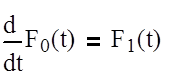тогда система диф. уравнений первого порядка запишется следующим  образом:

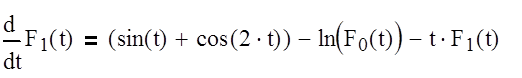(7)

                                                                      .

Тогда можно записать вектор первых производных

 

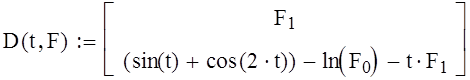,                (8)

для решения исходного дифференциального уравнения с помощью функции  rkfixed .

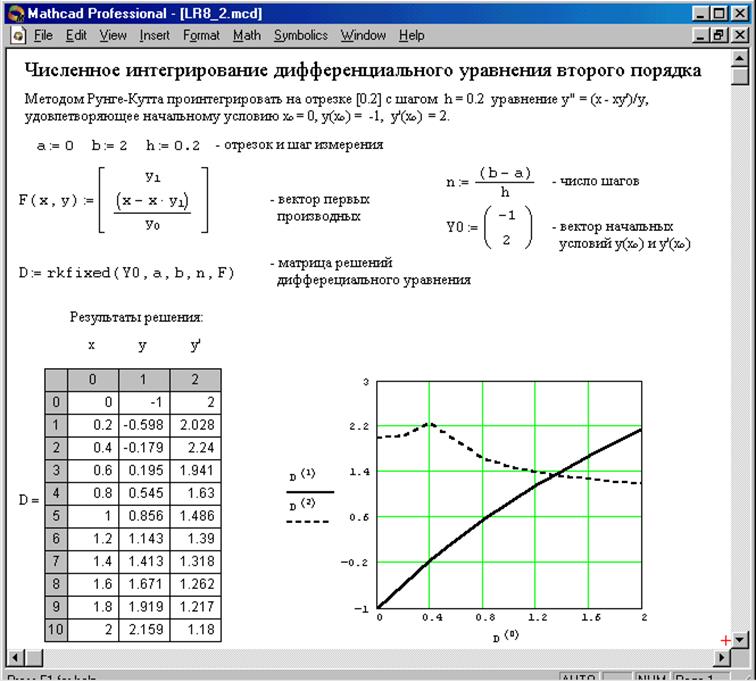
Рис. 9. Решение дифференциального уравнения второго порядка

Задание. Используя метод Рунге – Кутта четвертого порядка найти численное решение дифференциального уравнения второго порядка.

y'' = f(x,y,y'),

удовлетворяющих начальным условиям x₀ = 0, y(x₀) = y₀, y'(x₀) = z₀ на отрезке [a,b]. Шаг h = 0,05. Построить график решения.

Правая часть равнения, y₀, y₀' и границы участка a и b заданы в таблице 4.

Таблица 4

Номер варианта	f(x,y,y')	a	y0	y0'	b
1	–(y' + 1)/(1 + x)	3	1	1	4
2	(y'2 - x)/y	1	-1	1	2
3	sin(2 x) – y' tg(x)	1	-1	1	2
4	–(y'2 – y y')/(x y)	1	2	1	2
5	(y2 ln(y) – y'2)/y	1	2	1	2
6	(exx2 + y')/x	1	-1	1	2
7	–(y'2 + 1)/(1 + x2)	3	1	1	4
8	(2x + y')/y	1	1	1	2
9	y'2/(x + y)	0	1	2	1
10	–y'2/(x – y)	0	-1	2	1
11	(y' – 1)/(1 + x)	1	0	2	2
12	(y' – y)/(x + y)	1	1	2	2
13	(x2 + xy')/(1 + x2)	0	1	1	1
14	(1 + y')/(xy)	1	1	1	2
15	y'/(x ln(x))	2	1	1	3
16	(x3 – 2xy)/(1+x2)	0	1	1	1
17	(y2y' + x)/y	3	2	1	4
18	y' ln(y'/x)/x	1	1	1	2
19	2y'2 / tg(y)	1	2	1	2
20	(x + y')/(x + y)	1	1	2	2

Контрольные вопросы:

1)  Назовите несколько численных методов решения дифференциального уравнения.

2)  Назовите функции MathCADа предназначенные для решения дифференциальных уравнений.

БИБЛИ0ОГРАФИЧЕСКИЙ СПИСОК

1.  Дьяконов В.П., Абраменкова И.В. Mathcad 8 PRO в математике, физике и Internet. М.:Нолидж, 1999., -512 с.

2.  Плис А.И., Сивина Н.А. "MathCAD : математический практикум для экономистов и инженеров". М: Финансы и статистика. 1999. -656 с.

3.  Дьяконов В.П., Абраменкова И.В. Mathcad 7.0  в математике, физике и Internet. М.:Нолидж, 1998., -352 с.

4.  Дьяконов В.П. Справочник по MathCAD PLUS 7.0 PRO. – М.: СК ПРЕСС. – 1998, -352 с,

5.  МаthCAD 6.0 PLUS. Финансовые, инженерные и научные расчеты в среде Windows 95.- М.: Информ. изд. дом "Филинъ", 1996.- 712 с.