Методические указания к лабораторным работам по курсу “Информатика” (пакет MathCAD, часть 2), страница 4

rkfixed(y₀, x1, x2, N, f) – функция поиска решения диф. уравнения f методом Рунге-Кутта 4-го порядка в интервале [x1, x2] для N точек с начальным условием y₀.

Рис. 7. Численное интегрирование диф. уравнений 1-го порядка

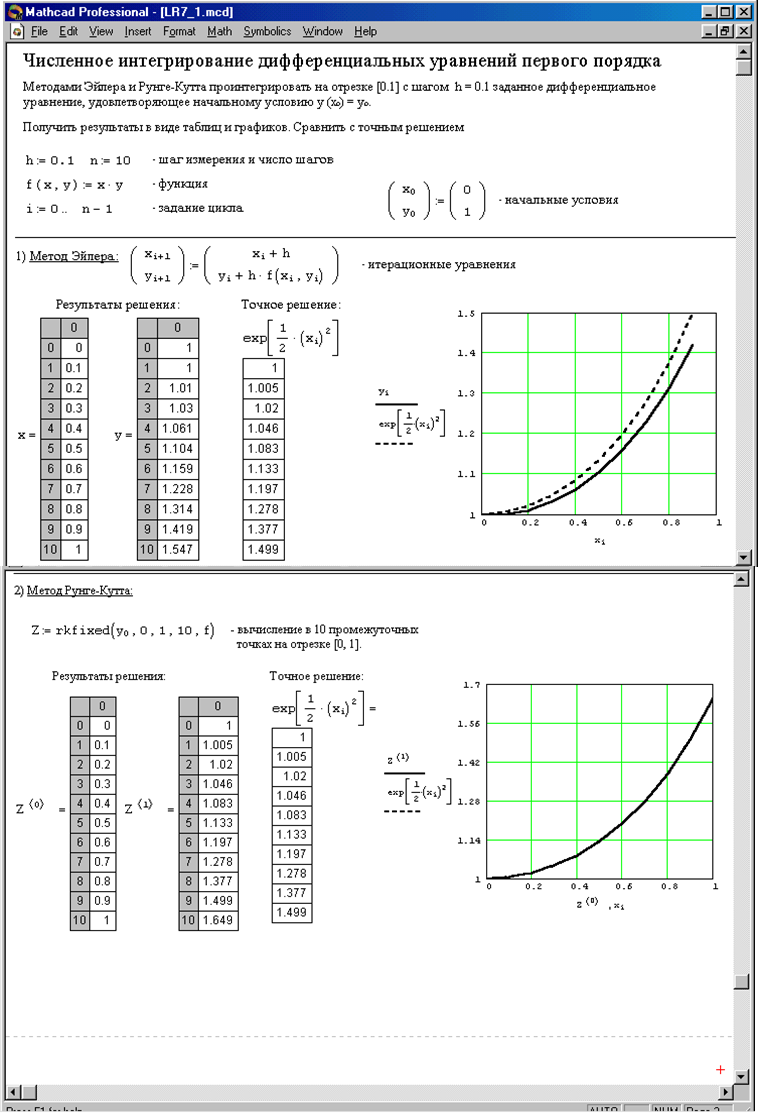Задание. Методами Эйлера и Рунге-Кутта проинтегрировать на отрезке [0.1] с шагом  h = 0.1 заданное дифференциальное уравнение (таблица 2), удовлетворяющее начальному условию у (х_о) = у_о. Получить результаты в виде таблиц и графиков. Сравнить с точным решением.

Таблица 2

Номер варианта	Дифференциальное уравнение	Начальное условие	Точное решение
1	у¢ = 2 ху	у (0) = 1	у =
2		у (0) = 1	у = ln (x + e)
3		y (0) = 1
4	у¢ = - у ех	у (1) =
5	у¢ = - 2 у + 4 х	у (0) = - 2	у = 2х - 1 - е-2х
6	у¢ = cosx - y	y (0) =
7	y¢ = y - 4x + 3	y (0) = 3	y = 2 ex + 4x + 1
8		y (0) = 1
9		y (1) = 0	y = (x - 1) / x
10		y (0) = 0	y =
Продолжение таблицы 2   11	y¢ = y + x	y (0) = 1	y = 2 ex - x - 1
12	y¢ =	y (1) = 2	y = x2 + x
13	у¢ = 2 х + 3х2	у (0) = 4	у = х2 + х3 + 4
14	у¢ =  3х2   - 2 х	у (2) = 4	у = х3 - х2
15		у (0) = 2
16		у (1) = 1	у = ln (x × y) + x
17		у (0) = 1	y =  ex
18		у (0) = 3
19		у (1) = e	y = x3 × ex
20		у (2) = 1

Контрольные вопросы:

1)  В чем состоит отличие аналитического и численного решения задачи Коши.

2)  Чем определяется погрешность численного решения дифференциального уравнения.

ЛАБОРАТОРНАЯ РАБОТА  8

РЕШЕНИЕ СИСТЕМ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ I^-ГО ПОРЯДКА.

Порядок решения системы дифференциальных уравнений методом Эйлера соответствует описанному в лабораторной работе 7.

Рис. 8. Решение системы дифференциальных уравнений

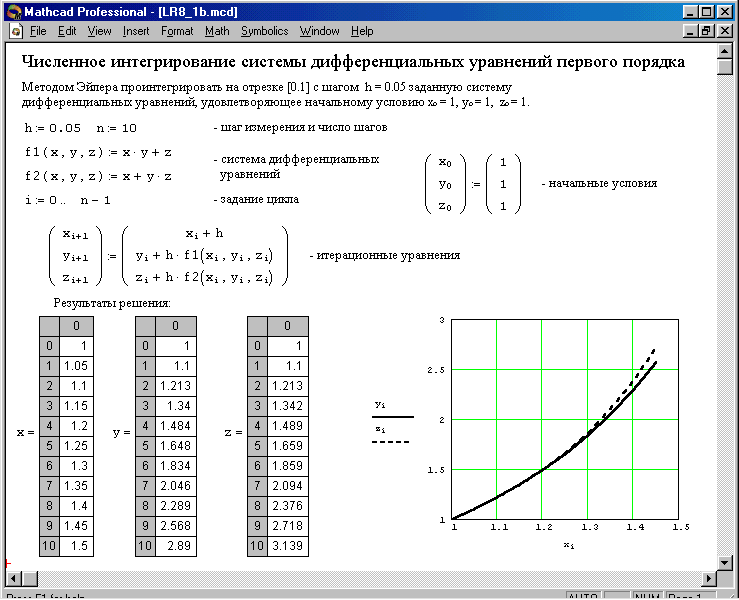Задание.  Используя метод Эйлера найти приближенное решение системы дифференциальных уравнений.

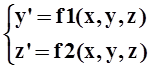
удовлетворяющих начальным условиям x = x₀, y(x₀) = y₀, z(x₀) = z₀ на отрезке [a,b]. Шаг h = 0,05. Построить график решения.

Первые части уравнений f1(x,y,z), f2(x,y,z), начальные условия и границы участка a и b заданны в таблице 3.

Таблица 3

Номер варианта	f1(x,y,z)	f2(x,y,z)	a = x0	y0	z0	b
1	1 + x + xy + z	x + y +z	0	0	0	0.3
2	x2 + y + z	x + y – 2z	1	2	3	1.3
3	2x + y	x + z + y	0	0	0	0.3
4	z2 + x/y	(x + y)/2	1.5	2.5	3	1.8
5	x3 + z	x2 + y2	0	0	0	0.5
6	2x – 3y + z	x – y – z	0	0	1	0.3
7	xy – z	x – yz	1	1	3	1.3
8	x – y	y + z – x	0	0	0	0.4
9	x – 2y2	x3 + xy	0.5	0	0	0.8
10	y + z + sin(x)	cos(x) + y	1	1	0	1.4
11	ln(x) + y + z	sin(x) + y	1	0	1	1.3
12	3x + z	x + y – z	1	0	2	1.5
13	tg(x) + y	x + y + z	2	3	3	2.6
14	x – tg(y)	y – x + z	1	2	4	3.5
15	sin(x) – y – z	x + sin(y) + z	3	2	3	1.6
16	x + y + z2	x – 2z	1	2	-3	1.6
17	sin(x) + y	cos(x) + z	1	-2	-2	1.5
18	sin(x) + xy	x + y	1	-2	0	1.8
19	2x – 3y	y + z2	1	2	4	0.6
20	x – 0.5y + 2	x - y	0	2	4	2.5