Лабораторная работа № 12. Профилирование кулачка.

Лабораторная работа № 12

Профилирование кулачка

     Цель работы: построение профиля кулачка по заданной схеме кулачкового механизма и заданному закону движения толкателя.

     Оборудование: прибор для профилирования кулачка ТММ-21, бумажный круг.

Общие положения

Кулачковые механизмы дают возможность реализовать любой закон движения ведомого звена (толкателя) при равномерном движении ведущего звена (кулачка). Наибольшее распространение получили механизмы с вращающимся кулачком (рис. 12.1, а, б).

Рис. 12.1. Схемы кулачковых механизмов

В механизме с поступательно движущимся толкателем (рис. 12.1, а) при вращении кулачка 1 толкатель 3 перемещается на величину линейного перемещения s = 0...s_max, занимая при любой угловой координате кулачка положения, задаваемые законом движения. Контакт толкателя с кулачком может осуществлятьсяпо высшей паре трения скольжения (грибовидный, плоский толкатель либо толкатель, оканчивающийся острием) или для уменьшения потерь на трение — по высшей паре трения качения (ролик 2, рис. 12.1, а, б, конструктивно выполняемый в виде подшипника качения).

В механизме с качающимся толкателем (коромыслом) вращение кулачка 1 дает угловое перемещение коромысла 3 ψ = 0 ... ψ_max (рис. 12.1, б).

Исходные данные для проектирования (синтеза) кулачкового механизма:

а) схема кулачкового механизма;

б) закон движения толкателя;

в) максимальное перемещение толкателя s_max или ψ_max;

г) длина коромысла (для кулачково-коромыслового механизма);

д) максимально допустимый угол давления [] или минимально допустимый угол передачи [μ].

Синтез кулачкового механизма состоит из двух этапов:

   а) определение основных размеровкулачка по допускаемомууглу давления (передачи): начального радиуса r₀ и смещения e – для поступательно движущегося толкателя; начального угла ψ₀, межосевого расстояния а и начального радиуса r₀ - для кулачково-коромыслового механизма;

   б) профилирование, т.е. построение центрового (теоретического) и конструктивного (практического) профилей кулачка.

Цель данной работы – освоение второго этапа проектирования: построение профилей кулачка – профилирование кулачка.

Законы движения толкателя

Закон движения толкателя выбирают в зависимости от назначения кулачкового механизма (обеспечение заданной технологии либо приемлемых динамических нагрузок) в виде аналитических или графических зависимостей одного из кинематических параметров (перемещения, скорости или ускорения) от времени t или угла поворота кулачка φ. Другие кинематические зависимости получают в результате интегрирования или дифференцирования заданных функций.

Поскольку кулачковые механизмы большинства машин работают при высоких угловых скоростях кулачка, то для снижения инерционных нагрузок, действующих на звенья механизма, используют такой закон движения толкателя, чтобы его ускорения при работе механизма были минимальными. Поэтому при проектировании кулачковых механизмов обычно задают закон изменения ускорений, а диаграмму перемещений толкателя получают в результате двукратного интегрирования ускорений.

Безударная работа осуществляется при синусоидальном законе изменения ускорения (рис. 12.2, а). Кинематическую диаграмму можно разбить на четыре фазы, соответствующие углам поворота кулачка: φ_у — угол удаления, на котором толкатель совершает прямой ход, например, открытие клапана двигателя внутреннего сгорания; φ_д — угол дальнего стояния (выстой на максимальном перемещении); φ_с — угол сближения (закрытие клапана); φ_б — угол ближнего стояния (выстой в начальном положении). Весь цикл работы механизма соответствует одномуоборотукулачка:

Амплитуду диаграммы ускорений принять равной  = 40...50 мм. Косинусоиду строят по 7 точкам с ординатами ; 0,866; 0,5; 0; - 0,5 ; - 0,866; - . По оси абсцисс фазовые углы откладывают в масштабе μ_φ (мм/град):

где — длина отрезка на оси абсцисс, соответствующая рабочему профильному углу; рекомендуется принимать  = 150 мм.

Масштаб угла поворота  (мм/рад):

Слеваот оси ординат откладывают отрезок интегрирования Н₁ = 25 мм.

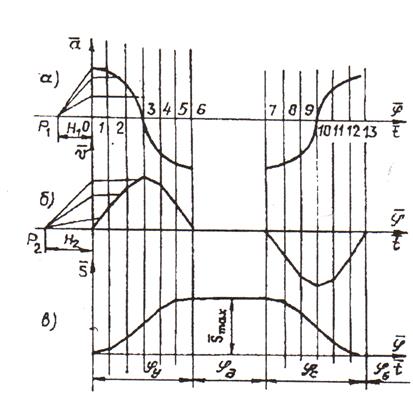
Рис. 12.3. Графическое интегрирование