Лабораторная работа № 2. Структурный анализ механизмов

Лабораторная работа №2

Структурный анализ механизмов

Цель работы: изучение моделей плоских рычажных механизмов, выполнение структурного анализа механизмов по заданной модели и по заданной схеме.

Оборудование: модели плоских рычажных механизмов; схемы механизмов.

Краткие теоретические сведения

Твердое тело, входящее в состав механизма, называется звеном. Механизм имеет одно неподвижное звено (стойку) и несколько подвижных звеньев. Подвижное соединение двух соприкасающихся звеньев называется кинематической парой. Кинематические пары классифицируют по числу степеней свободы (одноподвижная, двухподвижная и т.д.) и по виду элемента пары (низшая и высшая). Элемент высшей пары – это точка или линия, низшей – поверхность (цилиндрическая и сферическая) или плоскость.

Система звеньев, образующих между собой кинематические пары, называется кинематической цепью. В плоской кинематической цепи все подвижные звенья совершают плоское движение, параллельное одной и той же неподвижной плоскости. Число степеней свободы плоского механизма, равное числу начальных звеньев, определяют по формуле П.Л.Чебышева:

где n – число подвижных звеньев; р₁ – число низших кинематических пар (вращательных или поступательных); р₂ – число высших кинематических пар.

Начальному звену задают скорость и обобщённую координату – угол его расположения или линейную координату. Это ведущее звено в технологических машинах и ведомое в двигателях.

В примере плоского кривошипно-ползунного механизма (рис. 2.1) при n = 3, p₁ = 4 и p₂ = 0 число степеней свободы (число начальных звеньев) . Это означает, что для выполнения целесообразных движений необходимо поставить один двигатель.

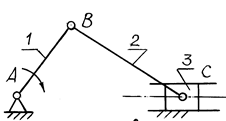
Рис. 2.1. Кривошипно-ползунный механизм

           Для пространственных механизмов число степеней свободы определяют по формуле А.П.Малышева:

где p₁, p₂ и т.д. – число одноподвижных (с одной степенью свободы), двухподвижных и т.д. пар.

Для целей классификации, а также облегчения структурного, кинематического и динамического анализа плоский механизм разделяют на структурные группы, которые также называют группами Ассура. Группа Ассура – плоская кинематическая цепь с числом степеней свободы, равным нулю. Она не содержит высших кинематических пар. С учетом приведенных признаков из формулы Чебышева выводят формулу группы Ассура:

Таким образом, в группе Ассура число звеньев может быть только чётным, а число кинематических пар кратно 3. Простейшая группа Ассура состоит из 2-х звеньев и 3-х кинематических пар. В более сложной группе 4 звена и 6 пар и т.д.

Класс группы Ассура определяют числом кинематических пар, входящих в наиболее сложный контур (звено или группу звеньев).

Порядок группы Ассура равен числу внешних (потенциальных) кинематических пар, которыми она может быть присоединена к стойке и подвижным звеньям. Примеры групп Ассура различных классов приведены в табл. 2.1.

Таблица 2.1. Группы Ассура

Простейшие группы Ассура называются двухповодковыми или диадами. В базовой диаде (1-го вида) все три кинематические пары – вращательные (рис. 2.2). Другие виды получают заменой одной или двух вращательных пар поступательными (рис. 2.3…2.6).

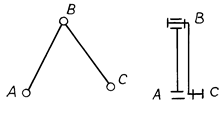
Рис. 2.2. Диада 1-го вида

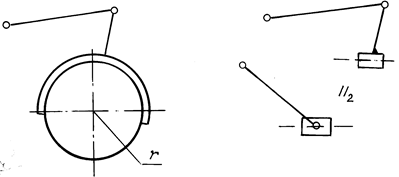
Рис. 2.3. Диады 2-го вида

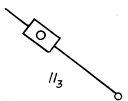
Рис. 2.4. Диады 3-го вида

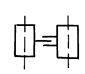
Рис. 2.5. Диады 4-го вида

Рис. 2.6. Диада 5-го вида

Цель структурного анализа — отсоединение групп Ассура по схеме механизма. После отсоединения остаются начальные механизмы I класса (рис. 2.7), число которых равно числу степеней свободы плоского механизма.

Рис. 2.7. Начальные механизмы I класса

Формулу строения механизма начинают с римской цифры I, символизирующей начальный механизм I класса. Её связывают линией с другой римской цифрой, определяющей класс соседней группы Ассура. В индексе указывают порядок группы  (в диадах — класс и вид, например II₁).

В зубчатых и кулачковых механизмах высшие пары заменяют низшими. Высшую пару заменяют одним  звеном с двумя низшими парами. При замене находят центры кривизны и ставят в них вращательные кинематические пары, которые соединяют звеном друг с другом и с ближайшими кинематическими парами (рис. 2.8).

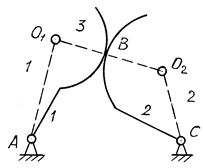
Рис. 2.8. Замена высшей пары низшими

Аналогичный пример замены высшей пары низшими в зубчатом зацеплении приведен на рис. 2.9.

В кулачковых механизмах с точечным контактом центр кривизны находится в точке контакта (рис. 2.10, б).

В коромысле, имеющем контакт по плоскости, радиус кривизны равен бесконечности. В этом случае вращательную пару заменяют поступательной. Дополнительным звеном будет ползун 3, выполненный заодно со стержнем О₃А (рис. 2.10, а).

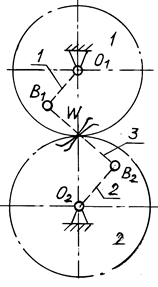
Рис. 2.9. Замена высшей пары в зубчатом зацеплении

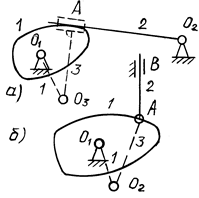
Рис. 2.10. Замена высшей пары в кулачковых механизмах

В кулачковых механизмах с роликом перед отсоединением групп Ассура ролик удаляют, так как он создает лишнюю степень свободы (вращение относительно собственной оси), не влияющую на кинематику. Кулачок при этом эквидистантно увеличивают на радиус ролика (рис. 2.11), вычерчивая штриховой линией центровой профиль.