САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ, МЕХАНИКИ И ОПТИКИ
ОТЧЁТ
ПО КОМПЬЮТЕРНОМУ ПРАКТИКУМУ
по теме:
ФОРМИРУЮЩИЕ ФИЛЬТРЫ
Выполнил
студент группы 3715 Курский А.Г.
Санкт-Петербург
2008
Задание
Основная часть
Формирующим фильтром (ФФ)– называется система, которая из белого шума (БШ) позволяет получить случайный процесс с заданными характеристиками.
|
|
|
|||||
БШ – это стационарный шум, спектральные составляющие которого одинаковы на всем диапазоне задействованных частот.
Амплитуда импульсов – случайная величина с мат. ожиданием равным нулю.
Алгоритм моделирования Белого Шума.
1. {γi} Є (0, 1); - где гамма – стандартное равномерное распределение
2. Центрируем величину
{xi}: xi= γi - ½ - тем самым добиваемся того, чтобы xi имело M=0;
3. {vi}:
vi = ![]()
Где Vi – белый шум; d– интенсивность БШ, которая равна его дисперсии M[v2(k)]=σ2=d.
y(k+2) – 0.8 y(k+1) + 0.16 y(k) = v(k)
y(k) – 0.8 y(k-1) + 0.16 y(k-2) = v(k)
y(k) = v(k) + 0.8 y(k-1) - 0.16 y(k-2)
y(k+2) – 0.8 y(k+1) + 0.16 y(k) = v(k)
считая z[ y(k+n) ] = zn [ y(k) ]
z2 y(k) – 0.8 z y(k) + 0.16 y(k) = v(k)
H(z) = 1/ (z2 – 0.8 z + 0.16)
H(z-1) = z2 / (0.16 z2 – 0.8 z + 1)
Sy(z) = H(z) Sv(z) H(z-1) (спектральная плотность выходного сигнала)
Sv(z) = σ2 = const
Вывод
White noise
мат ожидание: -0.0333
дисперсия: 1.3305
Y(k) Stohastic(37, 21, 21, 100)
мат ожидание: 0.1096
дисперсия: 1.2018
for i= 1:100
s(i) = 1.3305 * i *i / (0.16 * i^4) - 0.928 * (i^3) + 0.3856 * (i^2) - 0.928 * i + 0.16);
end;
plot (z, s)
Sy(z) = 1.3305 z2 / (0.16 z4 – 0.928 z3 + 0.3856 z2 – 0.928 z + 0.16)
Приложение
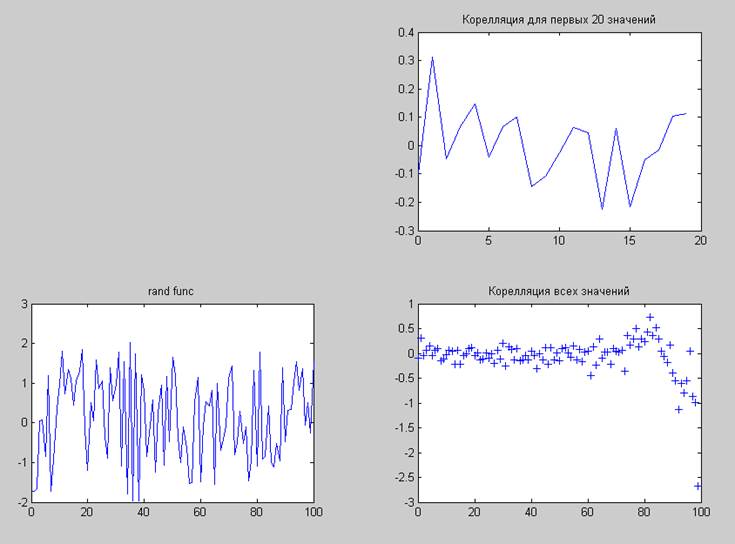
Рис. 1 – y(k)
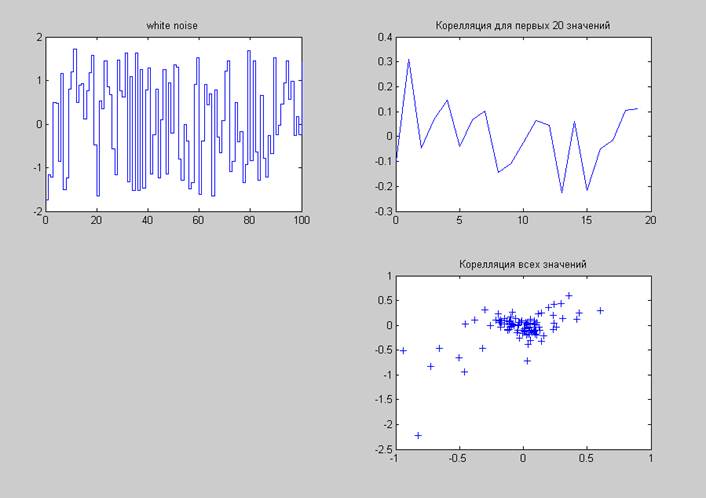
Рис. 2 – white noise
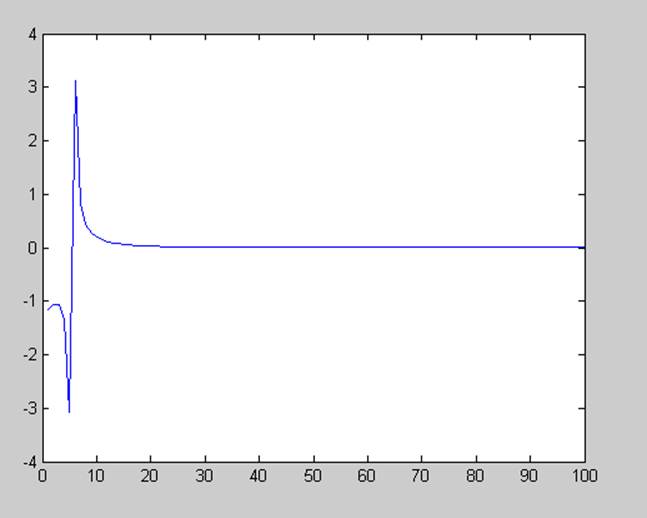
Рис. 3 – спектральная плотность
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.