|
|
|
i |
y |
x |
||
|
|
y1 |
x1 |
||
|
… |
… |
… |
||
|
n |
yn |
xn |
Параметризация модели - определение параметров выбранной формальной зависимости Y=a+bx2 на основе собранных статистических данных (табл.1).
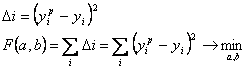 | |||
![]() Метод наименьших
квадратов применим к формальным векторам, которые линейны относительно своих
параметров
Метод наименьших
квадратов применим к формальным векторам, которые линейны относительно своих
параметров
 |
![]()
 |
|
|
Z |
U1 |
U2 |
… |
Un |
||
|
|
1 |
>0.8 |
>0.8 |
… |
>0.8 |
||
|
U1 |
|
1 |
|
|
|
||
|
U2 |
|
<0.8 |
1 |
|
|
||
|
… |
|
<0.8 |
|
1 |
|
||
|
Un |
|
>0.8 |
<0.8 |
|
1 |
Составляем матрицу парных коэффициентов корреляции:
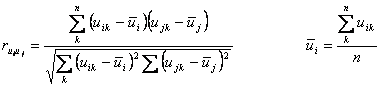 |
|
|
Z |
U1 |
U2 |
||
|
Z |
1 |
Zzu1³0.8 |
Zzu2³0.8 |
||
|
U1 |
Zu1z³0.81 |
1 |
Zu1u2<0.8 |
||
|
U2 |
|
|
1 |
а если связи нет, то |ruiuj| < 0.8
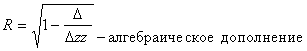 |
Детерминант D = R2 = 0.9 - показывает полноту охвата оценки.
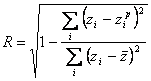 |
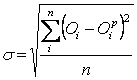 |
В каких диапазонах будут изменяться факторы ( доверительные интервалы повторить из математической статистики).
Пример:
Уi = (2,3,4,5)
У = [2,5] V=[500-1000]
Сетевая модель.
Достоинства линейного графика:
- простота построения
- наглядность
Сетевая модель - абстрактная модель, отражающая взаимосвязь сложного комплекса работ в их технологической последовательности с помощью ориентировочного графа.
Линейный график отражает всегда только одну характеристику.
Ориентировочный график - упорядоченное множество вершин (узлов) и ориентировочных дуг, соединяющие эти вершины.
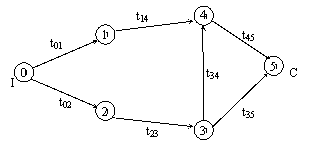 |
1) событий (кружочки - события, стрелки - их взаимосвязь),
2) работ (кружочки - работы),
3) событий и работ (кружочки - события и стрелочки - работы).
Термин работ имеет 3 значения:
1) действительная работа - реальный процесс, имеющий продолжительность и требующий исполнителей.
2) ожидание - реальный процесс, имеющий продолжительность, но не требует исполнителей, т.е. не имеет трудоемкость.
3) фиктивная работа или логическая связь - зависимость, которая не имеет продолжительности и не требует исполнителей.
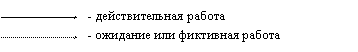 |
Событие - не имеет продолжительности, это момент времени начала и окончания какого-либо процесса.
Событие, которое не имеет ни одной предшествующей работы, называется исходным (I)
![]() Событие, которое
не имеет ни одной последующей работы, называется завершающим (С).
Событие, которое
не имеет ни одной последующей работы, называется завершающим (С).
 все остальные
события могут быть начальными или конечными.
все остальные
события могут быть начальными или конечными.
 |
Параметры сетевой модели.
1. Топология сети.
2. Длительность всех работ.
![]() У начального
события номер должен быть меньше, чем у конечного.
У начального
события номер должен быть меньше, чем у конечного.
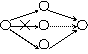 1) не должно быть
замкнутых контуров,
1) не должно быть
замкнутых контуров,
2) не должно быть тупиковых событий (их надо связать фиктивной работой),
3) не должно быть хвостовых событий,
 4)между двумя
событиями должна быть только 1 работа.
4)между двумя
событиями должна быть только 1 работа.
 | ||
 | ||
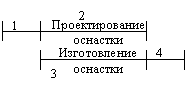
Полный путь - это весь путь сетевого графика, начало которого совпадает с исходным событием, а конец совпадает с завершенным событием.L(I-C)
Путь - вся последовательность (непрерывная) работ, в которой конечное событие каждой работы является начальным событием последующей работы.
Путь, предшествующий событиюi L(I-i) - начало совпадает с исходным событием, конец с событием i.
Путь, последующий за событием i - путь от данного события i до завершающего.
Критический путь - полный путь максимальной длины (продолжительности)
Подкритический путь - полный путь, который по длительности следует за критическим.
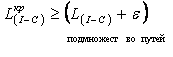 |
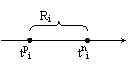
Событие имеет 3 параметра:
1) ранний срок свершения события tpi
2) поздний срок свершения события tпi
3) резерв времени события Ri
Параметры работы:
1) продолжительность работы tij
2) ранний срок начала работы tpнij
3) раннее окончание работы tpоij
4) позднее начало работы tпнij
5) поздний срок окончания работы tпоij
6) полный резерв времени работы Rnij
7) частный резерв времени I вида RIij
8) частный резерв времени II вида RIIij
9) свободный резерв времени Rсвij
10) коэффициент напряженности работы Kнij
 |
 |
Резерв времени события показывает на какой предельно допустимый период времени можно задержать срок выполнения события, не нарушая при этом срока выполнения комплекса работ, т.е. не увеличивая длительность критического пути.
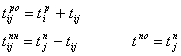 | |||
Линейный график:
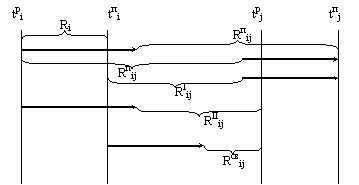 |
Полный резерв времени работы равен резерву максимального из путей, проходящего через работу.
Резерв события равен резерву максимального из путей, проходящего через это событие.
1. Если начальное событие какой-либо работы имеет критические пути, то ее полный резерв и частный резерв I вида совпадают.
2. Если конечное событие какой-либо работы имеет критические пути, то ее полный резерв и частный резерв II вида совпадают.
3. Если и начальное и конечное событие работы имеют критические пути, а сама работа не имеет его, то все 4 резерва совпадают.
Коэффициент напряженности работы - отношение продолжительностей максимально не совпадающих (но заключенных между одними и теми же событиями отрезков пути, одним из которых является критичный, а другим - путь максимальной продолжительности, проходящий через эту работу)
T(Lkp) - длительность критического пути
T`(Lkp) - длительность совпадающих отрезков путей Lкр и Lmax
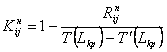 |
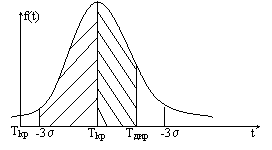
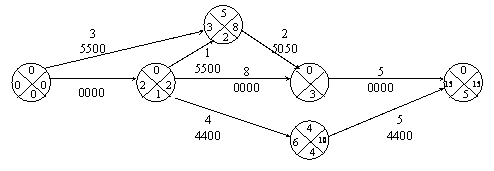
Tkp=15 дн. - случайная величина, характеризующаяся мат ожиданием и дисперсией
Ткр=t0-1 + t1-3 + t3-5
Dkp=D0-1 + D1-3 + D3-5 - дисперсия
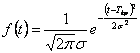 |
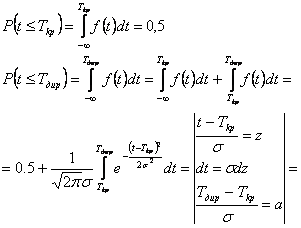 | |||
 |
 |
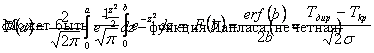 |
Линейная карта сети и график загрузки.
Линейная карта сети - это линейный график планируемого комплекса работ, который представляет собой сетевой график, перестроенный с учетом длительности выполняемых работ в определенном масштабе времени.
Правила построения линейной карты сети:
 |
2. по оси ординат откладываются без масштаба, а только качественно полные резервы работ
3. если же резервы равны, а работы разные, то тогда откладывают по коэффициентам напряженности в порядке убывания.
 |
|
 |
«Оптимизация» сетевого графика.
Под оптимизацией сетевого графика понимают улучшение параметров сетевой модели эвристическими методами.
Параметры сетевой модели, которые могут быть улучшены:
|
2. n=max{nK} , к- интервал
Задачи:
1. уменьшить Ткр,
2. уменьшить необходимое количество исполнителей для каждой работы,
3. одновременное уменьшение Ткр и n.
1. уменьшение Ткр.
![]()
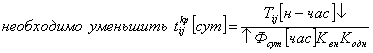 |
окончание раздела «Техническая подготовка производства».
 | |||
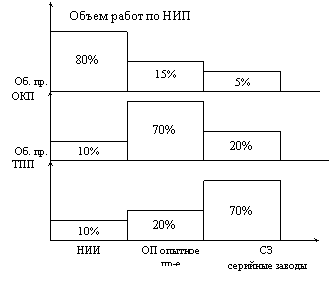 | |||
Планирование программы выпуска предприятия.
Основа внутризаводского планирования - это программа, которая определяет наличие, виды ресурсов и т.д.
 |
Каждое агрегатно-сборочное предприятие выступает как самостоятельное предприятие, имеющее определенную мощность (площади, оборудование) и деньги. Оно может поставлять продукцию нескольким предприятиям.
Имеется n-изделий однородных в конструкторско-технологическом отношении. Каждое изделие характеризуется трудоемкостью, материалоемкостью и характеризуется рыночной ценой.
Xi - объем выпуска i -изделия.
|
Изд-е |
1 |
… |
j |
… |
n |
|
t |
t1 |
|
tj |
|
tn |
|
m |
m1 |
|
mj |
|
mn |
|
c |
c1 |
|
cj |
|
cn |
|
|
x1 |
… |
xj |
… |
xn |
 |
 |
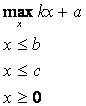 |
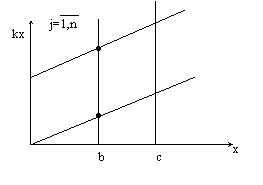 пример:
пример:
Ответ: x=b
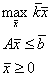 |

Ответ не изменяется, а меняется целевая функция, ее значение.
в двойственной задаче меняется:
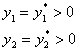 |
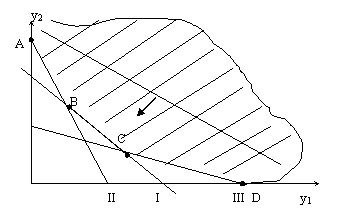 | ||
 | ||
С(С)- min.
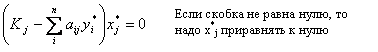 |
 |
при изменении цены будет меняться решение задачи, т.е.N2, N3…
|
|
|
|
|
|
|
П11 |
П12 |
П13 |
|
|
П21 |
П22 |
П23 |
|
|
П31 |
П32 |
П33 |
Это решается с помощью теории игр. игрок.N1..3,-максимизирующий,
С1…3 - минимизирующий. Это игра с нулевой суммой, т.е. то, что выиграет один игрок, обязательно проиграет другой.
 |
2. определить стратегию в соответствии с критерием.
1. Критерий Лапласа соответствует принципу недостаточного основания.
2. Принцип гарантированного результата или критерий Вальда.
В каждой строчке выберем наихудший результат max min, затем из них максимальное
 3. Принцип
Гурвица. Выбираем наилучшую строку maxПij затем берем средневзвешенную сумму
3. Принцип
Гурвица. Выбираем наилучшую строку maxПij затем берем средневзвешенную сумму
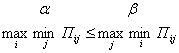 4. По теории
Вальда
4. По теории
Вальда
 |
самый высокий и минимумов и самый низкий из Гулливеров
N1p1+N2p2+N3p3
Смешанная стратегия - распределение вероятностей по стратегиям
Необходимо определить p1, p2, p3 - часть продукции в общей сумме (или вероятность в теории игр)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.