Функция H(iω) равна отношению преобразований Фурье выходной и входной функций.
Замечание. В соотношении(17) реакция системы Y(t) в момент времени t зависит от значений функции на входе как в момент времени s<t, так и в момент времени s>t. В физических устройствах это невозможно, поэтому для них h(t,s) =0 для всех s>t.Это условие называют условием физической осуществимости системы. Таким образом, функцию h(t,s) следует определить так:
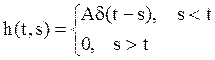 (18)
(18)
Вернемся к задачам нашего параграфа. Пусть на вход
системы (16) поступает СП Х(t) с математическим ожиданием ![]() и корреляционной функцией
и корреляционной функцией ![]() .Выходной процессY(t)
тогда имеет вид :
.Выходной процессY(t)
тогда имеет вид : 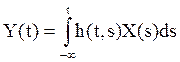 .
Найдем
.
Найдем ![]() и
и ![]() .
.
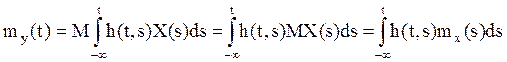 (21)
(21)
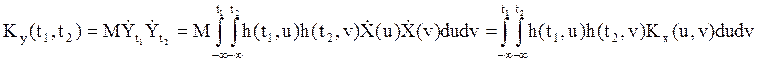 (22)
(22)
Если СП Х(t) стационарен, то
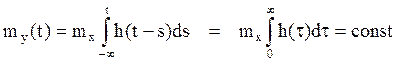
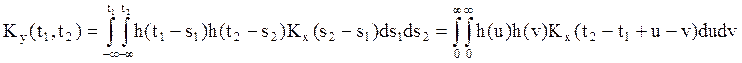 =
=
= 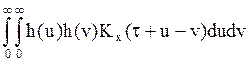 или
или
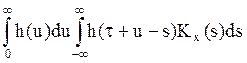 (23)
(23)
Таким образом , если на вход подается стационарный ( хотя бы в широком смысле)
процесс, то на выходе процесс также стационарен ( хотя бы в широком смысле).
Вычислим спектральную
плотность процесса Y(t) : 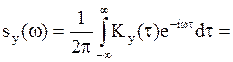
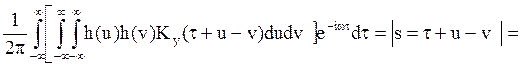
= 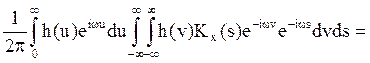
![]() .
.
Итак, ![]() (24)
(24)
Найдем 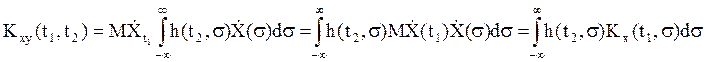 . (25)
. (25)
Для стационарного процесса X(t) получим формулу
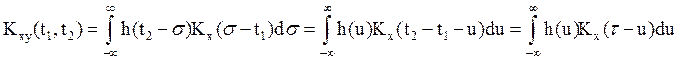 (26)
(26)
При вычислении
интеграла сделали замену ![]()
Обратимся теперь к
вычислению взаимной спектральной плотности ![]() процессов
X(t) и Y(t). Пусть X(t)
представим стохастическим интегралом (формула 13):
процессов
X(t) и Y(t). Пусть X(t)
представим стохастическим интегралом (формула 13): 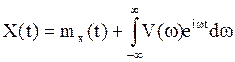 , а
, а
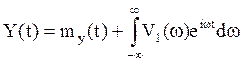 .
Тогда
.
Тогда 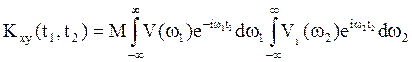 =
=
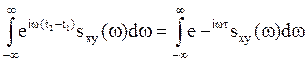 ,таким
образом,
,таким
образом,
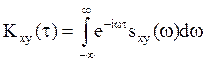 (27)
(27)
Взаимная спектральная
плотность обладает следующими свойствами, вытекающими из свойства 2
спектральной плотности: 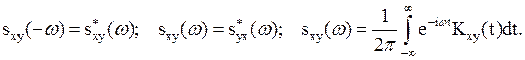 Итак,
Итак,
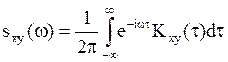 .
(28)
.
(28)
С учетом равенства (28)
формула (27 ) принимает вид 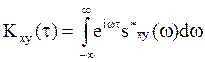
С другой стороны, 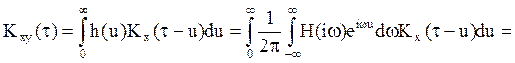
![]() =
= 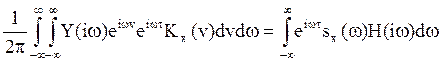 , здесь η=
, здесь η=![]()
Сравнивая полученные выражения для взаимных ковариационных функций, получаем:
![]() , то есть
, то есть
![]() (29)
(29)
Рассмотрим применение общих закономерностей , полученных выше, к частным случаям.
1.
Пусть ![]() , то
есть
, то
есть 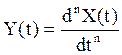 в среднем квадратичном смысле.
в среднем квадратичном смысле.
По формуле (21) имеем ![]() .
Если X(t) стационарный СП ,то
.
Если X(t) стационарный СП ,то ![]() =0
уже при n=1.
=0
уже при n=1.
По формуле (22) имеем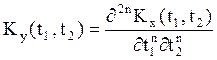 . Если
X(t) стационарный СП , то
. Если
X(t) стационарный СП , то
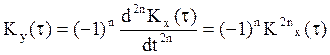 (30)
(30)
Найдем ![]() с помощью формулы (30):
с помощью формулы (30):
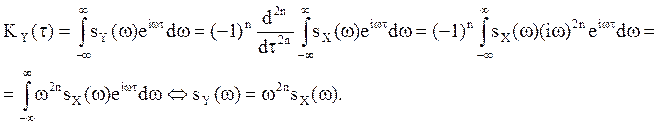 (31)
(31)
Законность интегрирования под знаком интеграла следует из существования n-ой производной процесса X(t) , что равносильно сходимости несобственного интеграла
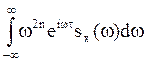 .
.
2. Пусть 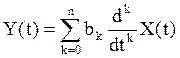 ,
, ![]() , и
, и ![]() -
известные постоянные, k=0,1,…n, и X(t)- скалярный стационарный СП, n раз
дифференцируемый на
-
известные постоянные, k=0,1,…n, и X(t)- скалярный стационарный СП, n раз
дифференцируемый на ![]() , со спектральной плотностью
, со спектральной плотностью ![]() . Знаем , что любой ССП представим в виде
стохастического интеграла
. Знаем , что любой ССП представим в виде
стохастического интеграла 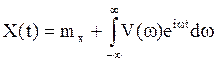 . Тогда Y(t) –
скалярный стационарный СП
. Тогда Y(t) –
скалярный стационарный СП 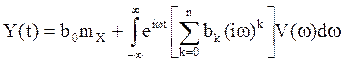 ,
, ![]() , поскольку
, поскольку 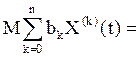
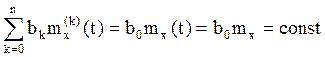 . По
условию X(t) n раз с.к. дифференцируемый процесс , то
. По
условию X(t) n раз с.к. дифференцируемый процесс , то 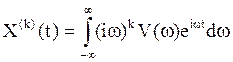 , к=1,… n Тогда
, к=1,… n Тогда
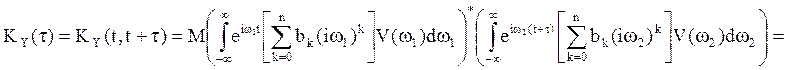
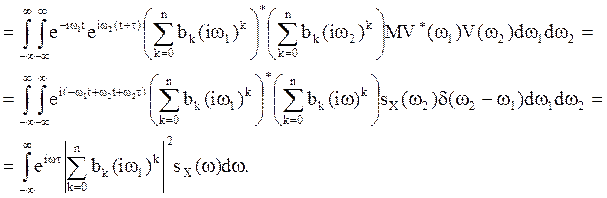
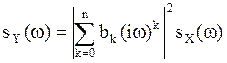 (32)
(32)
3. Рассмотрим достаточно общий случай преобразований стационарного СП при его прохождении через линейную динамическую систему.
Пусть X(t), ![]() , - стационарный n раз с.к.
дифференцируемый на Т скалярный СП с математическим ожиданием
, - стационарный n раз с.к.
дифференцируемый на Т скалярный СП с математическим ожиданием ![]() и спектральной плотностью
и спектральной плотностью ![]() , а скалярный СП Y(t),
, а скалярный СП Y(t), ![]() , m раз с.к. дифференцируем на Т
и имеет место соотношение:
, m раз с.к. дифференцируем на Т
и имеет место соотношение:
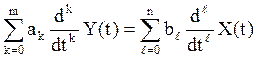 ,
, ![]() , (33)
, (33)
в котором ![]() ,
, ![]() -
известные постоянные.
-
известные постоянные.
При достаточно
больших ![]() , когда в системе затихли переходные
процессы и система начинает работать в установившемся режиме, СП Y(t),
, когда в системе затихли переходные
процессы и система начинает работать в установившемся режиме, СП Y(t), ![]() , можно считать скалярным стационарным СП с
математическим ожиданием
, можно считать скалярным стационарным СП с
математическим ожиданием ![]() , спектральной плотностью
, спектральной плотностью
![]() .
.
Имеем в этом
случае ![]()
![]()
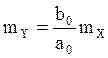 , (34)
, (34)
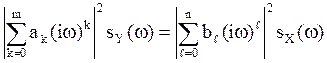
![]()
![]() ,
(35) где функция
,
(35) где функция 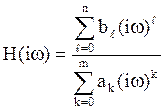 носит название частотной характеристики
динамической системы, описываемой уравнением (33).
носит название частотной характеристики
динамической системы, описываемой уравнением (33).
Результаты (34),(35) могут быть получены рассуждениями, аналогичными рассуждениям предыдущего пункта 2.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.