Ковариационная функция ![]() непрерывна, кусочно монотонна на
отрезке
непрерывна, кусочно монотонна на
отрезке ![]() , а значит, имеет на отрезке ограниченное
изменение, в концах отрезка имеет равные значения, следовательно, по признаку
Дирихле ее ряд Фурье равномерно к ней сходится:
, а значит, имеет на отрезке ограниченное
изменение, в концах отрезка имеет равные значения, следовательно, по признаку
Дирихле ее ряд Фурье равномерно к ней сходится:
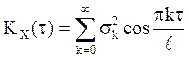 ,
где
,
где 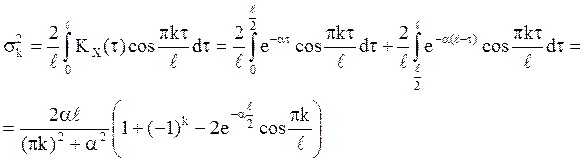
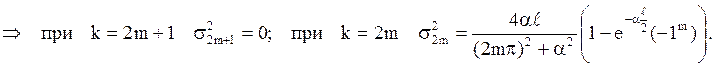
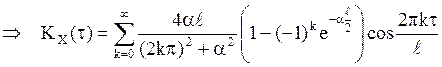 и
тогда по теореме СП X(t),
и
тогда по теореме СП X(t), ![]() , представим рядом
Фурье.
, представим рядом
Фурье.
4.3.2. Стационарные случайные функции с непрерывным спектром
Результаты предыдущего
параграфа можно представить в ином виде. Введем в рассмотрение функцию 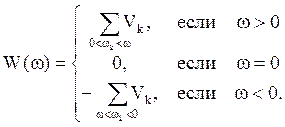
Функция ![]() - ступенчатая функция с некоррелированными
случайными скачками в фиксированных точках
- ступенчатая функция с некоррелированными
случайными скачками в фиксированных точках ![]() , иначе
говоря,
, иначе
говоря, ![]() - СПНРП,
- СПНРП, ![]() ,
, ![]() . Как отмечалось в
. Как отмечалось в ![]() такие
процессы описываются функцией
такие
процессы описываются функцией ![]() , которую в этой главе
мы переобозначим:
, которую в этой главе
мы переобозначим: ![]() ,
,
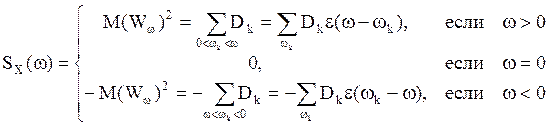 и
и ![]() . Функция
. Функция ![]() также
ступенчатая функция со скачками в точках
также
ступенчатая функция со скачками в точках ![]() . Ее
производная
. Ее
производная ![]() представляет собой линейную комбинацию
представляет собой линейную комбинацию ![]() -функций с коэффициентами
-функций с коэффициентами ![]() :
:
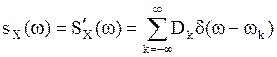 (6)
(6)
Формулу (1) теперь
запишем как 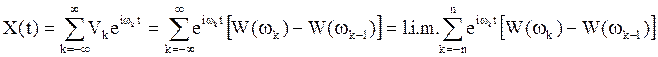 . Сумму под знаком с.к. предела
можно рассматривать как интегральную сумму для функции
. Сумму под знаком с.к. предела
можно рассматривать как интегральную сумму для функции ![]() по
СПНРП
по
СПНРП ![]() . С учетом формулы (2) выражение для
. С учетом формулы (2) выражение для ![]() можно рассматривать как с.к. предел
интегральных сумм для функции
можно рассматривать как с.к. предел
интегральных сумм для функции ![]() по ступенчатой функции
по ступенчатой функции ![]() :
:
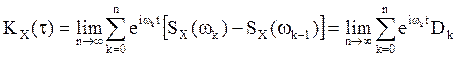 .
.
Теперь формулы (1) и (2) можно переписать в виде
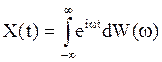 (7)
(7)
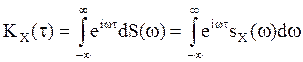 (8)
(8)
При этом необходимым и достаточным условием сходимости стохастического интеграла (7) является сходимость интеграла (8)( см. раздел 3.9).
Поработаем с формулой (6).
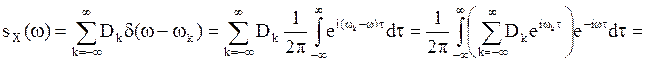
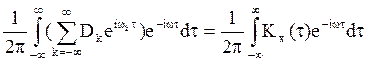 .
Итак,
.
Итак,
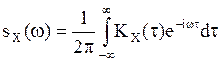 (9)
(9)
Здесь использовано
преобразование Фурье для функции![]()
![]() =
= 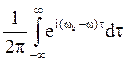 . Равенства (9) и (8) означают, что
функции
. Равенства (9) и (8) означают, что
функции ![]() и
и ![]() связаны
взаимно обратными преобразованиями Фурье. Они обладают всеми свойствами ,
присущими этим преобразованиям. В частности, чем «шире»
связаны
взаимно обратными преобразованиями Фурье. Они обладают всеми свойствами ,
присущими этим преобразованиям. В частности, чем «шире» ![]() ,
тем « уже»
,
тем « уже» ![]() ( заметим, что при условии
( заметим, что при условии ![]() , функция
, функция ![]() совпадает
с функцией
совпадает
с функцией ![]() ).
).
Отметим еще, что
интеграл (9) понимается в смысле главного значения и только, если ![]() - абсолютно интегрируемая функция,
интеграл (9) – обычный несобственный интеграл.
- абсолютно интегрируемая функция,
интеграл (9) – обычный несобственный интеграл.
Соотношения (8),(9) называют теоремой Винера- Хинчинадля ССП.
Из соотношения (6) :
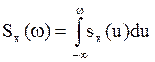 (10)
(10)
Из соотношения (8):
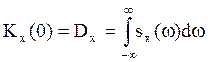 (11)
(11)
В различных
приложениях теории СП величину ![]() зачастую
интерпретируют как “энергию” скалярного ССП, а
зачастую
интерпретируют как “энергию” скалярного ССП, а ![]() - как плотность энергии на единицу частоты.
Термин “энергия” обязан своим появлением реализациям СП в
электротехнике(напряжение или силаэлектрического тока). Энергия электрического
тока пропорциональна квадрату энергии, приходящейся в среднем на
гармоническое колебание частоты ω.
- как плотность энергии на единицу частоты.
Термин “энергия” обязан своим появлением реализациям СП в
электротехнике(напряжение или силаэлектрического тока). Энергия электрического
тока пропорциональна квадрату энергии, приходящейся в среднем на
гармоническое колебание частоты ω.
Cпектральная
плотность как и корреляционная ( коввариационная ) функция служит
характеристикой СП , она используется при применении частотных методов
исследования стационарных систем. Однако это не независимая характеристика СП: ![]() и
и ![]() связаны
соотношением (9).
связаны
соотношением (9).
Подводя итог всему
сказанному выше в этом разделе, видим, что от представления СП в виде суммы
(1) можно перейти к его интегральному представлению (7), тем самым от
счетного множества частот {![]() } ,
характеризующих СП, к несчетному (непрерывному) множеству частот, также
определяющих этот процесс.
} ,
характеризующих СП, к несчетному (непрерывному) множеству частот, также
определяющих этот процесс.
Получим результаты
(8),(9) формально для любого ССП, представимого стохастическим интегралом (7).
Итак, пусть 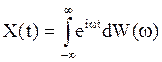 - некоторый скалярный ССП,
- некоторый скалярный ССП, ![]() - СПНРП с нулевым математическим ожиданием
и
- СПНРП с нулевым математическим ожиданием
и ![]() с вероятностью 1, имеющий конечный момент
2 порядка. Вспомним формулу (7)
с вероятностью 1, имеющий конечный момент
2 порядка. Вспомним формулу (7) ![]() : именно так связаны
функции
: именно так связаны
функции ![]()
![]() в формуле (10),
следовательно,
в формуле (10),
следовательно, ![]() является интенсивностью
СПНРП
является интенсивностью
СПНРП ![]() , а
, а ![]() - его
ковариацинной функцией. Тогда согласно формуле 10
- его
ковариацинной функцией. Тогда согласно формуле 10 ![]() :
:
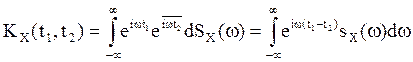 , или
полагая
, или
полагая ![]() ,
, 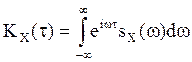 -
получили формулу (8) настоящего раздела. Из нее немедленно следует формула (11), которая
в свою очередь означает, что
-
получили формулу (8) настоящего раздела. Из нее немедленно следует формула (11), которая
в свою очередь означает, что ![]() конечна тогда и только
тогда, когда интеграл (11) сходится. Но это же условие ( сходимость интеграла
(11)) необходимо и достаточно для существования стохастического интеграла (7)
или для представления СП
конечна тогда и только
тогда, когда интеграл (11) сходится. Но это же условие ( сходимость интеграла
(11)) необходимо и достаточно для существования стохастического интеграла (7)
или для представления СП ![]() в виде стохастического
интеграла (7) ( см.
в виде стохастического
интеграла (7) ( см. ![]() ).
).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.